Deep Multi Task y Meta Learning

Aquí intento tener una visión general del uso y aplicaciones sobre Deep Multi Task y Meta Learning, procedente del curso de Standford.

1. Definiciones

1.1 Multi-Task Learning

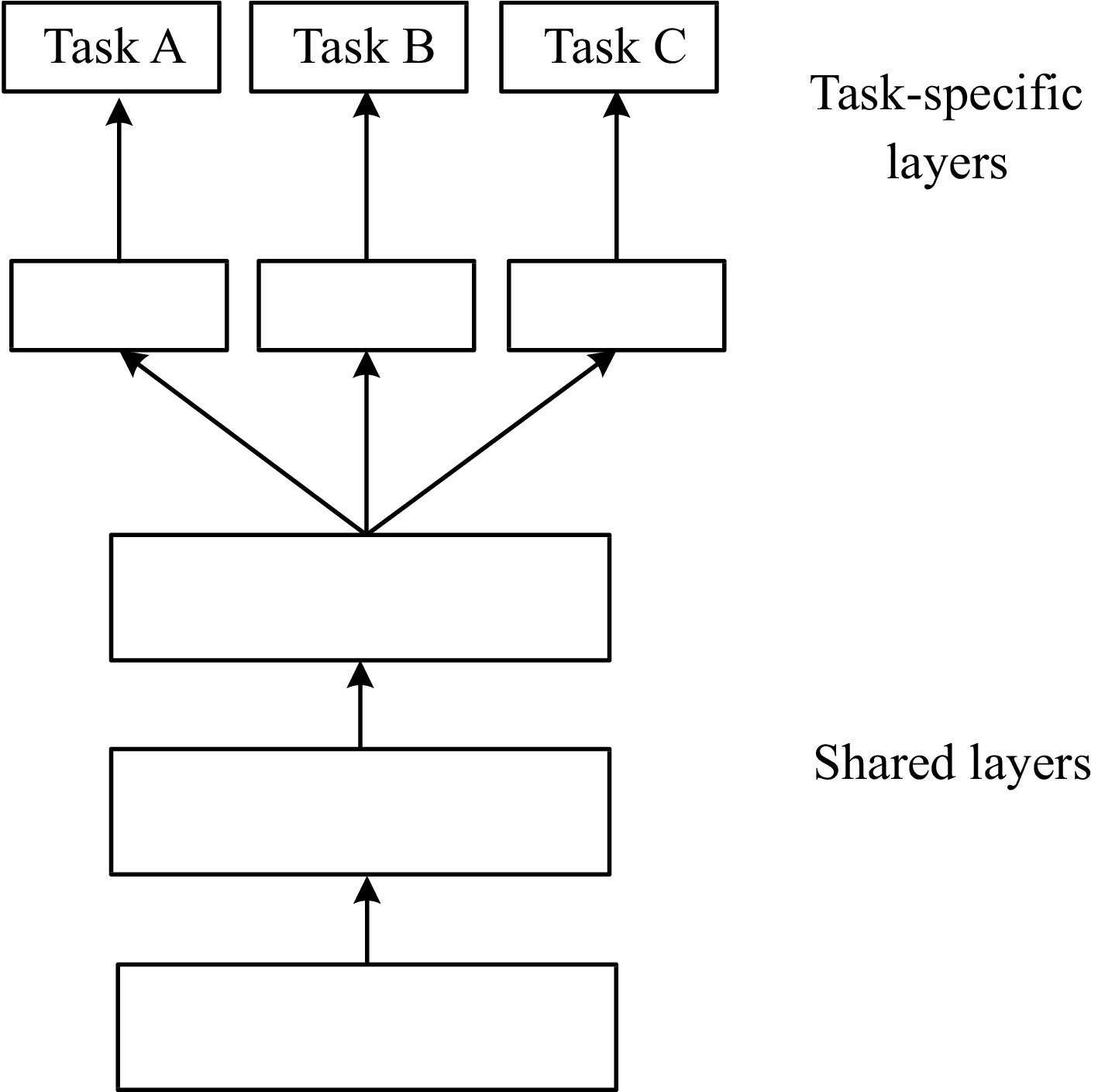
Diagrama de una arquitectura Multi-Task

El Multi-Task Learning (MTL) se refiere a la capacidad de un modelo para realizar múltiples tareas relacionadas de forma simultánea, utilizando una estructura compartida que permite adaptar parámetros y salidas según el entorno.

Este enfoque busca optimizar recursos y mejorar la capacidad de generalización del modelo en escenarios dinámicos, transfiriendo conocimiento entre tareas y minimizando la necesidad de ajustes específicos. Un ejemplo de aplicación es el aprendizaje por refuerzo.

1.2 Meta-Learning

Diagrama sobre el uso de Meta-Learning

El Meta-Learning se enfoca en dotar a los modelos de la habilidad de identificar y aprovechar patrones subyacentes en los datos, lo que les permite adaptarse rápidamente a nuevos problemas o entornos con un mínimo de información.

Este enfoque es particularmente útil en escenarios con datos limitados o costosos de obtener, como aquellos que involucran problemas de privacidad. Al mejorar la capacidad de generalización, los modelos son más robustos y eficientes, optimizando recursos y ofreciendo mejores resultados en tareas variadas.

Por tanto, resulta ideal para conjuntos de datos donde la proporción de datos etiquetados es significativamente menor que la de datos no etiquetados. El uso del paradigma de Meta-Learning permite extraer patrones de datos etiquetados y aplicarlos a datos no etiquetados, detectando variaciones y cambios en las distribuciones.

2. Parámetros en Multi-Task Learning

Al desarrollar modelos para multi-task learning, es crucial definir ciertos parámetros:

• Parámetros aprendibles, $\theta$: Representa todos los parámetros que el modelo puede aprender.
• Función, $f_\theta(y|x)$: Describe el modelo parametrizado $\theta$, generando una distribución de probabilidad para $y$ dado $x$.
• Tarea, $T_i$: Se define como $T_i = \{p_i(x), p_i(y|x), L_i\}$, donde:
  • $p_i(x)$: Distribución de entrada $x$ específica de la tarea $T_i$.
  • $p_i(y|x)$: Distribución de probabilidad de la salida $y$ dado $x$ para la tarea $T_i$.
  • $L_i$: Función de pérdida asociada con la tarea $T_i$.

El objetivo general es minimizar la pérdida total del modelo a lo largo de todas las tareas. Esto se puede formular como

$$\min_{\theta} \sum_{i=1}^{T} L_i(\theta, D_i),$$

donde $D_i$ es el conjunto de datos de la tarea $i$. Además, para ajustar la relevancia de cada tarea, se puede incluir un peso $w_i$

$$\min_{\theta} \sum_{i=1}^{T} w_i \cdot L_i(\theta, D_i).$$

2.1 Estrategias para Multi-Tasking

Las principales estrategias para abordar múltiples tareas incluyen:

1. Modelos específicos para cada tarea: Este enfoque no es escalable debido al alto costo computacional.
2. Uso de embeddings condicionales: Técnicas que combinan información mediante:
   • Concatenación o suma de embeddings: Métodos equivalentes que combinan características.
   • Sistemas Multi-head: Un modelo único con múltiples salidas, eficiente para tareas variadas. Un ejemplo avanzado es el Multi-Gate Mixture of Experts.
   • Condicionales multiplicativos: Ajustan los embeddings mediante factores multiplicativos según la tarea.

3. Meta-Learning

3.1. Aprendizaje Contrastivo

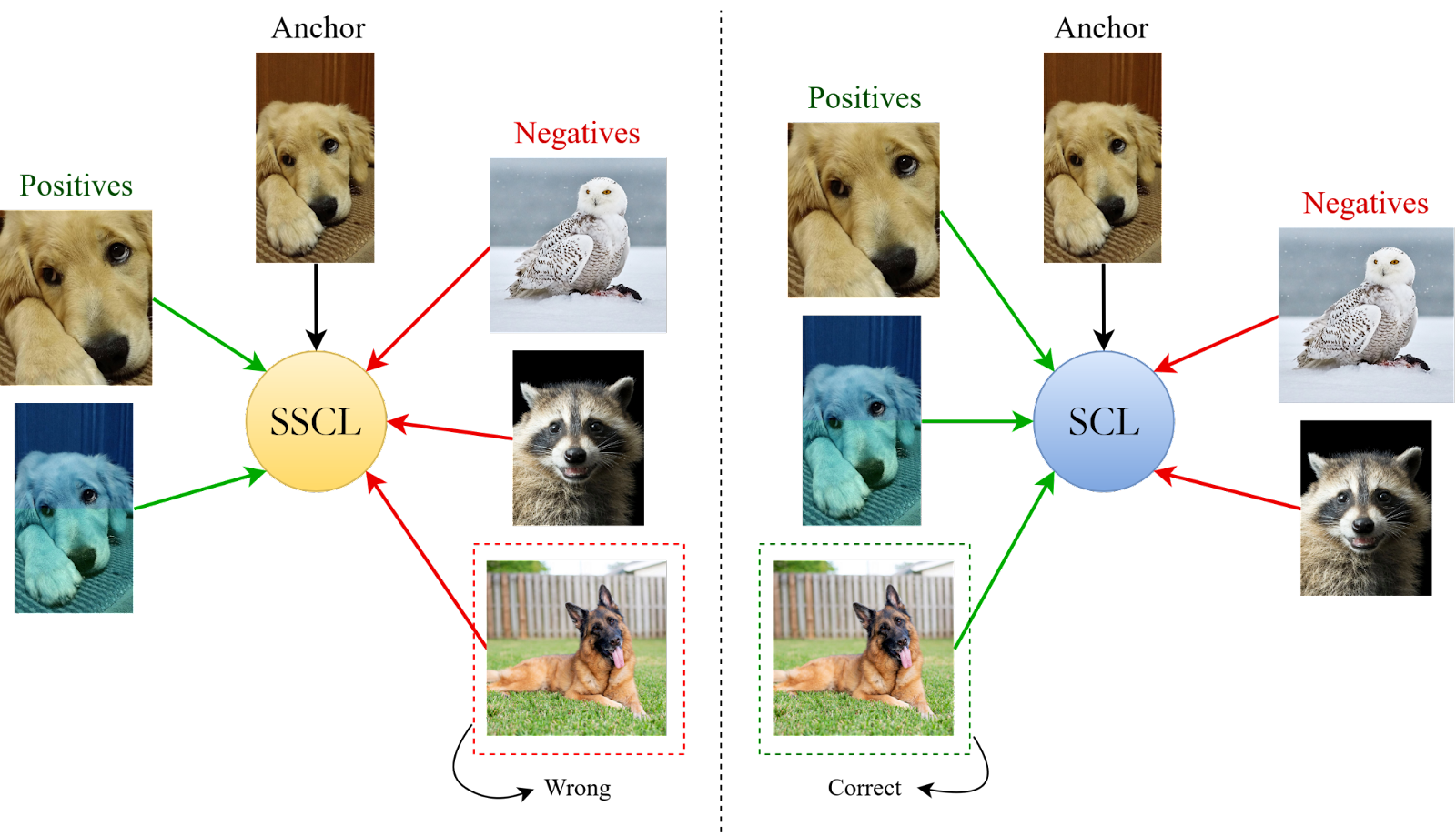
Ejemplo de Aprendizaje Contrastivo

El Aprendizaje Contrastivo es una técnica que, aunque no es exactamente lo mismo que el meta-learning, contribuye a la mejora de las representaciones en los modelos de aprendizaje profundo. Su objetivo principal es agrupar representaciones de datos similares y alejar aquellas que pertenecen a clases diferentes en el espacio embebido del modelo.

Por ejemplo, en aplicaciones de visión computacional, se utilizan transformaciones de los datos para que el modelo aprenda a reconocer que ciertas variaciones no alteran la esencia de la información original, mejorando la comprensión semántica y robusteciendo el modelo ante datos fuera de distribución.

3.1.1. Proceso de entrenamiento contrastivo

El proceso de entrenamiento contrastivo es una metodología clave para obtener representaciones efectivas y discriminativas a partir de datos no etiquetados. Este enfoque involucra varias etapas esenciales que, junto con técnicas de fine-tuning y transfer learning, optimizan el rendimiento del modelo.

1. El primer paso es la obtención de un conjunto de datos no etiquetados, que proporciona la base sobre la cual el modelo aprenderá automáticamente las características más relevantes.

2. A continuación, se procede con la generación de embeddings. Aquí, se emplea un modelo preentrenado, como una red neuronal profunda previamente ajustada en tareas generales con gran cantidad de datos, por ejemplo, ResNet en el ámbito de la visión computacional. Este modelo preentrenado ayuda a transformar los datos de entrada en representaciones de menor dimensionalidad que capturan las características más importantes de los datos originales, facilitando su estudio.

3. La fase de optimización mediante fine-tuning es crucial para refinar las representaciones. El objetivo es ajustar los parámetros del modelo usando métodos de cálculo de distancias entre embeddings, como la distancia euclidiana o la similitud de coseno. La idea es minimizar la pérdida contrastiva, que busca maximizar la cercanía de las representaciones de datos similares y, al mismo tiempo, aumentar la separación de las representaciones de datos distintos. Esto se logra utilizando funciones de pérdida específicas, como la Triplet Loss, que optimiza la distancia entre un ancla, un par positivo, y un par negativo; o la InfoNCE Loss, que es especialmente útil en escenarios no supervisados. Sin embargo, es esencial evitar el colapso de las representaciones, un problema donde todos los embeddings se vuelven indistinguibles. Para prevenirlo, se deben asegurar diferencias suficientes entre las clases.

4. Después de entrenar el modelo, se entra en la etapa de iteración y ajuste manual. Aquí, las muestras con mayores pérdidas se revisan y, si es necesario, se realiza un etiquetado manual. Esto refina aún más el modelo, permitiendo un ciclo iterativo en el que las predicciones mejoran progresivamente y la necesidad de intervención humana se reduce con el tiempo.

Este proceso de ajuste se basa en gran medida en los principios de Transfer Learning, que permiten reutilizar el conocimiento de una tarea fuente $T_a$ para mejorar el desempeño en una tarea objetivo $T_b$.

En lugar de empezar desde cero, se aprovechan las características generales ya aprendidas por el modelo preentrenado, lo que reduce la carga computacional y acelera el entrenamiento. Incluso si las distribuciones de datos de las tareas $T_a$ y $T_b$ son diferentes, estas características siguen siendo valiosas, ya que encapsulan información esencial, como bordes y texturas en imágenes o relaciones semánticas en datos textuales.

En algunos casos, el fine-tuning no se limita a ajustar únicamente la capa final del modelo. Estudios como el Surgical Fine-Tuning han demostrado que afinar selectivamente las capas intermedias puede mejorar significativamente la precisión.

3.1.2. Métodos de Aprendizaje Contrastivo

El aprendizaje contrastivo se ha vuelto fundamental en la mejora de las representaciones en diversos dominios, especialmente en visión computacional y procesamiento del lenguaje natural. A continuación, detallamos algunos de los métodos más utilizados.

Triplet Loss

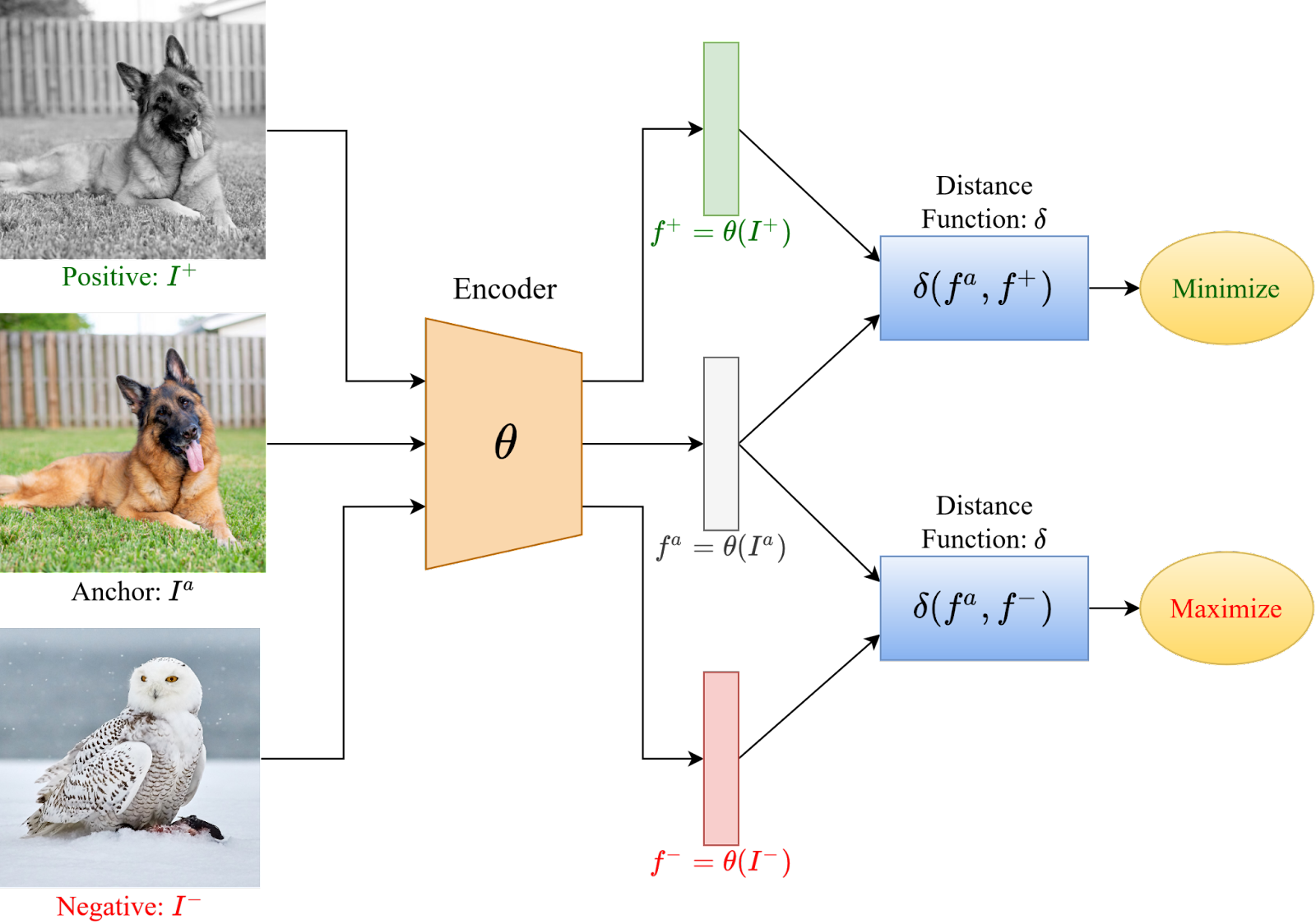
Ejemplo de Triplet Loss

La Triplet Loss se basa en tres componentes principales:

• Ancla ($X$): Una muestra de datos que sirve como referencia.
• Par positivo ($X^+$): Una muestra que es similar al ancla (pertenece a la misma clase o es un dato transformado del ancla).
• Par negativo ($X^-$): Una muestra que es distinta al ancla (pertenece a una clase diferente).

La idea detrás de Triplet Loss es minimizar la distancia entre el ancla y el par positivo, mientras se maximiza la distancia entre el ancla y el par negativo. Esto se define matemáticamente como

$$L = \min_{\theta}\left(\max\left(0, \text{dist}(X, X^+) - \text{dist}(X, X^-) + \text{margen}\right)\right),$$

donde:

• $\text{dist}(\cdot, \cdot)$: Es una función de distancia, como la distancia euclidiana o la similitud del coseno.
• margen: Un valor positivo que define cuánto mayor debe ser la distancia entre el ancla y el par negativo en comparación con la distancia entre el ancla y el par positivo.

La función de pérdida se activa cuando $\text{dist}(X, X^+)$ no es significativamente menor que $\text{dist}(X, X^-)$ más el margen. Este margen actúa como un umbral para garantizar que los pares negativos estén adecuadamente separados de los pares positivos, evitando el colapso de las representaciones. Sin el margen, las distancias podrían converger sin crear diferencias útiles en las representaciones.

Contrastive Loss

Otra función de pérdida clave en el aprendizaje contrastivo es la Contrastive Loss, que se usa en pares de datos (en lugar de tríos). Aquí, el objetivo es minimizar la distancia entre datos similares y maximizarla para datos diferentes. La fórmula se expresa como:

$$L = (1 - y) \frac{1}{2} \left( \text{dist}(X_1, X_2) \right)^2 + y \frac{1}{2} \left( \max(0, m - \text{dist}(X_1, X_2)) \right)^2,$$

donde:

• $y$: Es una etiqueta binaria que indica si $X_1$ y $X_2$ son similares ($y = 0$) o diferentes ($y = 1$).
• $m$: Es un margen que define la distancia mínima deseada entre ejemplos disímiles.
• $\text{dist}(X_1, X_2)$: Es típicamente la distancia euclidiana.

En este método, si los ejemplos son similares ($y = 0$), la pérdida se calcula como la distancia al cuadrado, forzando a los puntos similares a estar más cerca en el espacio embebido. Por otro lado, si los ejemplos son diferentes ($y = 1$), se busca que la distancia entre ellos sea al menos igual al margen $m$. Si ya están suficientemente alejados, la pérdida se reduce a cero.

InfoNCE Loss

El InfoNCE Loss (Noise-Contrastive Estimation) es otra función de pérdida utilizada comúnmente, especialmente en modelos como SimCLR. Este método maximiza la similitud de un dato ancla con sus pares positivos y minimiza la similitud con pares negativos en el mismo lote de datos. La fórmula es:

$$L = -\frac{1}{N} \sum_{i=1}^N \log \frac{\exp(\text{sim}(z_i, z_i^+)/\tau)}{\sum_{j=1}^K \exp(\text{sim}(z_i, z_j^-)/\tau)},$$

donde:

• $z_i$: Es el embedding del dato ancla.
• $z_i^+$: Es el embedding del par positivo.
• $z_j^-$: Representa los embeddings de los pares negativos.
• $\text{sim}(\cdot, \cdot)$: Es una función de similitud, como el producto escalar o la similitud coseno.
• $\tau$: Es una constante de temperatura que controla la distribución de las probabilidades.

InfoNCE Loss maximiza la probabilidad de que el ancla esté cerca de su par positivo en comparación con los pares negativos dentro de un mismo lote. Esto fomenta que el modelo aprenda representaciones significativas y distintivas para diferentes clases o categorías.

3.1.3. Limitaciones del Aprendizaje Contrastivo

• Dependencia de transformaciones adecuadas: Se requieren técnicas específicas (como resizes, crops, ajustes de color, CutMix, y MixUp) para mejorar la robustez del modelo.
• Necesidad de un gran número de épocas: El rendimiento depende del tamaño del lote y el número de iteraciones para obtener suficientes pares negativos efectivos.

3.2. Few-Shot Learning

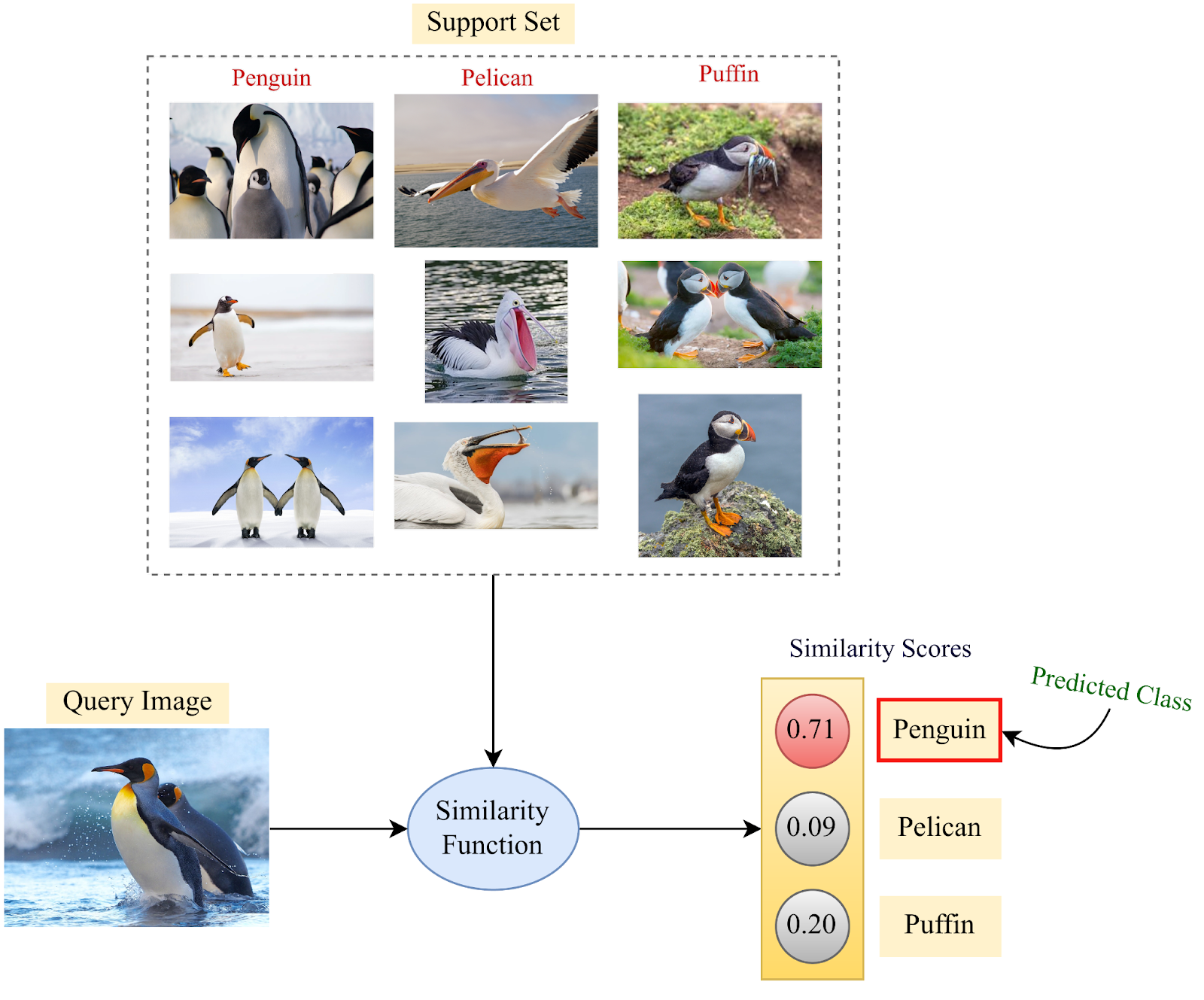
Ejemplo de uso de Few-Shot Learning de 3-ways y 3-shots

El Few-Shot Learning (FSL) se centra en entrenar modelos que logren un alto rendimiento con un número muy limitado de ejemplos etiquetados por clase. Este enfoque es esencial en situaciones donde la recopilación de datos es complicada o costosa, como en aplicaciones médicas o donde se requiere la privacidad de los datos.

El FSL se organiza en torno a dos conjuntos principales:

• Support Set: Es el conjunto de datos de entrenamiento específico para una tarea, compuesto por unas pocas muestras etiquetadas que el modelo utiliza para aprender a clasificar.
• Query Set: Es el conjunto de datos de prueba utilizado para evaluar el rendimiento del modelo en la misma tarea.

El aprendizaje few-shot se describe según dos parámetros importantes:

• K-shot Learning: Se refiere al número $K$ de ejemplos disponibles por clase en el support set. Por ejemplo, en un escenario de 1-shot learning, hay solo un ejemplo por clase, mientras que en 5-shot learning hay cinco ejemplos por clase.
• N-way Classification: Indica el número $N$ de clases diferentes en la tarea. Por ejemplo, un problema de 5-way classification implica clasificar entre cinco posibles categorías.

Existen dos tipos de modelos en este regimen:

• Modelos no parametrizados: Métodos como k-Nearest Neighbors (k-NN) son simples y eficaces cuando se dispone de pocos datos. Sin embargo, su eficacia depende de tener embeddings de alta calidad que representen bien las relaciones entre los datos.
• Modelos parametrizados: Redes neuronales profundas o métodos similares se utilizan para generar embeddings que capturan las características relevantes de los datos en un espacio de menor dimensionalidad, reduciendo problemas como la maldición de la dimensionalidad. Estos modelos se entrenan para producir representaciones invariantes a transformaciones y adecuadas para métodos como k-NN.

3.3. Modelos basados en reconstrucción

Los modelos basados en reconstrucción, como los Autoencoders, se utilizan para aprender representaciones compactas de los datos mediante la reconstrucción de las entradas originales a partir de una versión comprimida (el embedding). Sin embargo, en el contexto de few-shot learning, estos modelos enfrentan desafíos significativos. Una de las principales limitaciones es la tendencia a la memorización, lo que significa que los modelos pueden recordar ejemplos específicos sin capturar adecuadamente las características generales necesarias para la generalización.

Para mejorar el rendimiento de los autoencoders en few-shot learning, se implementan varias estrategias:

• Introducción de ruido: Agregar ruido a los datos de entrada durante el entrenamiento (como en los Denoising Autoencoders) fuerza al modelo a aprender representaciones más robustas, en lugar de memorizar ejemplos específicos.
• Imponer esparsidad (sparsity): Se introducen restricciones en la representación comprimida, como imponer esparsidad, para que solo las características más esenciales se mantengan activas. Esto ayuda a evitar que el modelo dependa de demasiados detalles irrelevantes.
• Decoders de menor capacidad: Utilizar decoders con menor capacidad obliga al encoder a aprender representaciones más útiles, ya que el decoder no puede compensar la falta de información simplemente "recordando" detalles específicos de las entradas.

Estas mejoras buscan que los autoencoders sean más eficaces en contextos de datos limitados, obligando al modelo a generalizar mejor y a crear representaciones más informativas. Sin embargo, incluso con estas mejoras, los autoencoders pueden no ser ideales para todas las aplicaciones de few-shot learning, y a menudo se prefieren enfoques más sofisticados que exploten mejor las relaciones en pocos ejemplos.