Machine Learning

1. Introducción

1.1. Definición

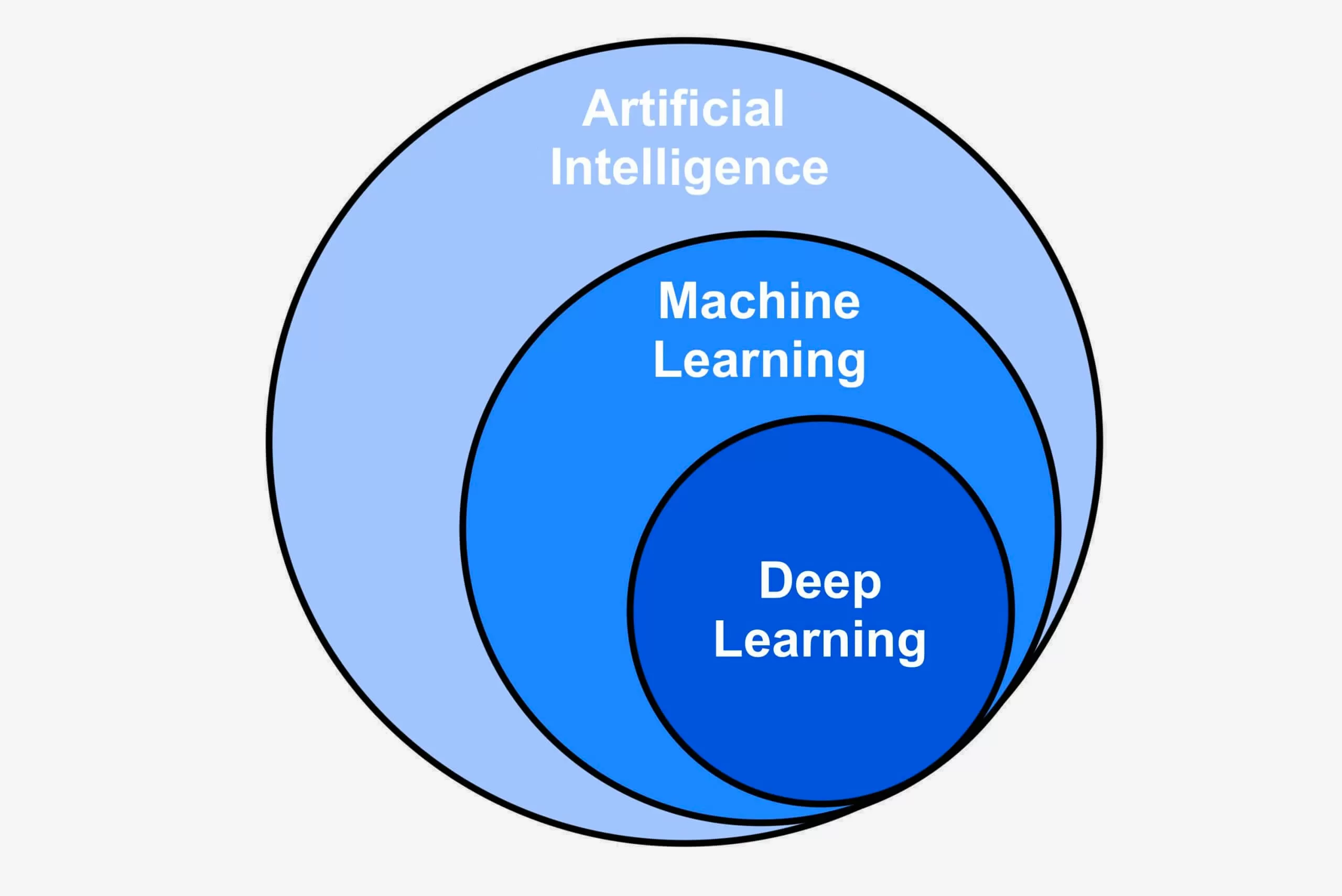
Ilustración sobre los conjuntos que engloba la inteligencia artificial. Link

El aprendizaje automático es una rama de la inteligencia artificial que se centra en el desarrollo y uso de algoritmos, también denominados modelos, capaces de identificar y comprender patrones en los datos de entrada con el objetivo de optimizar una métrica establecida.

A diferencia de los enfoques tradicionales de programación, donde las reglas se definen explícitamente, en el aprendizaje automático los algoritmos ajustan sus parámetros automáticamente para mejorar su desempeño en función de los datos.

1.2. Técnicas

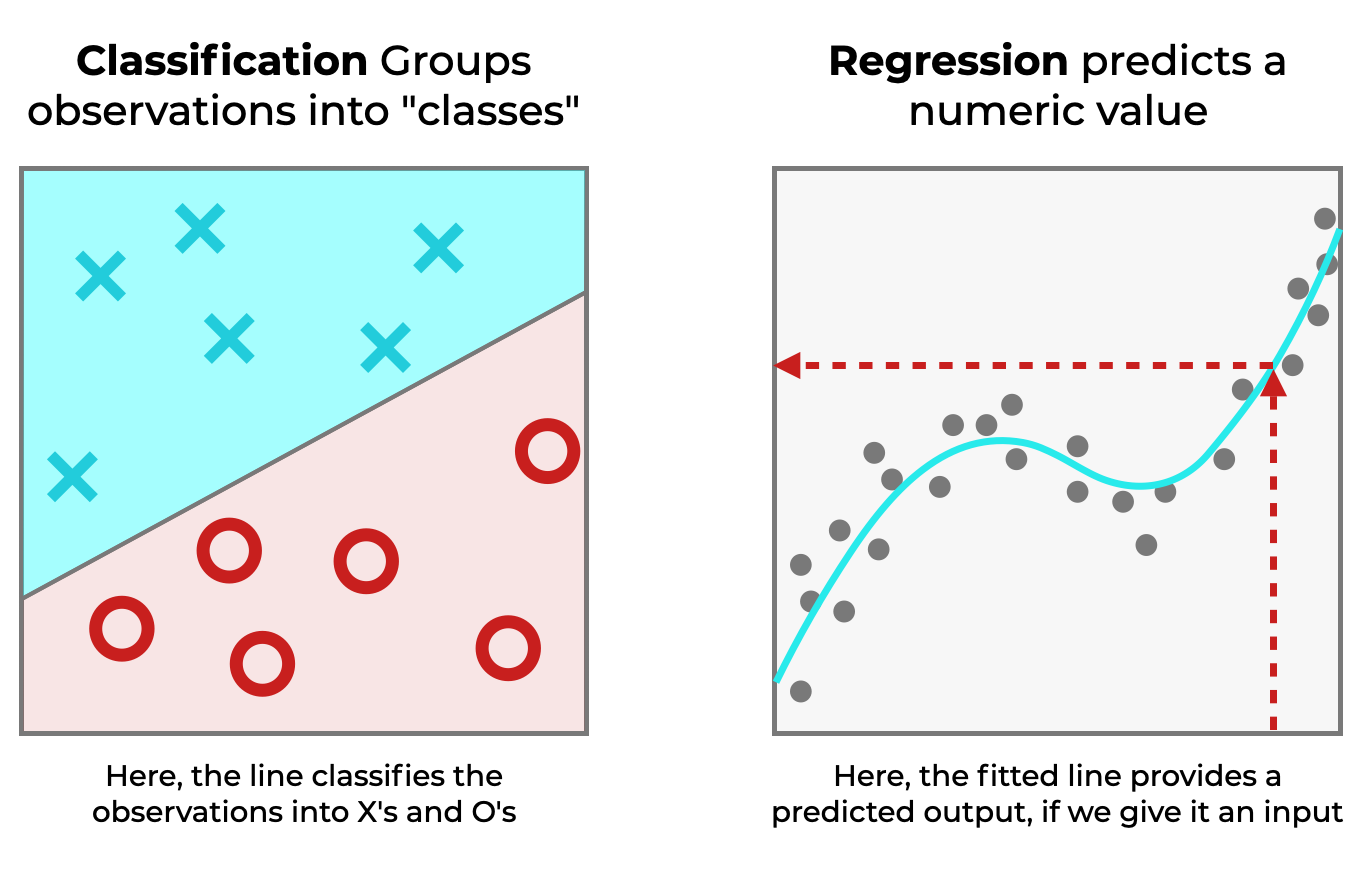
Clasificación vs Regresión. Link

Entre las técnicas más utilizadas se encuentran la clasificación y la regresión. La clasificación permite asignar etiquetas o categorías a los datos en función de sus características comunes. Un ejemplo de clasificación es la identificación del tipo de planta a partir de atributos como el ancho y la altura de sus hojas. Por otro lado, la regresión se emplea para realizar predicciones numéricas, como la estimación del precio de una vivienda en función de sus características.

La elección de la técnica adecuada depende de la naturaleza del problema. Un enfoque común consiste en evaluar múltiples algoritmos viables y compararlos para determinar cuál ofrece el mejor rendimiento. Esta comparación se basa en métricas de desempeño obtenidas a partir de los datos.

El proceso de entrenamiento de los modelos requiere dividir el conjunto de datos en distintas partes: una para el entrenamiento del modelo, otra para la evaluación de su desempeño y, en algunos casos, una tercera partición para validar su capacidad de generalización antes de su implementación en entornos reales. Durante este proceso, el algoritmo analiza las relaciones entre las características de los datos, identifica patrones y genera predicciones que se comparan con los valores reales. La diferencia entre las predicciones y las observaciones se mide mediante una métrica de error, lo que permite ajustar el modelo en cada iteración o época, es decir, cada vez que el algoritmo analiza completamente el conjunto de datos.

Ejemplo de subajuste, ajuste adecuado y sobreajuste. Link

Un modelo puede presentar sobreajuste (overfitting) cuando se ajusta demasiado a los datos de entrenamiento, logrando un alto rendimiento en estos pero fallando en datos nuevos. Este problema se conoce como el compromiso entre sesgo y varianza (bias-variance tradeoff), y su mitigación es esencial para obtener modelos que generalicen correctamente.

1.3. Tipos de datos

1.3.1. Variables dependientes e independientes

En un conjunto de datos, cada atributo que varía entre muestras se denomina variable. Si una variable depende de otra, se considera dependiente, en caso contrario, se clasifica como independiente. Las variables independientes, también llamadas características (features), son las utilizadas en el entrenamiento del modelo para predecir la variable dependiente.

1.3.2. Datos continuos y discretos

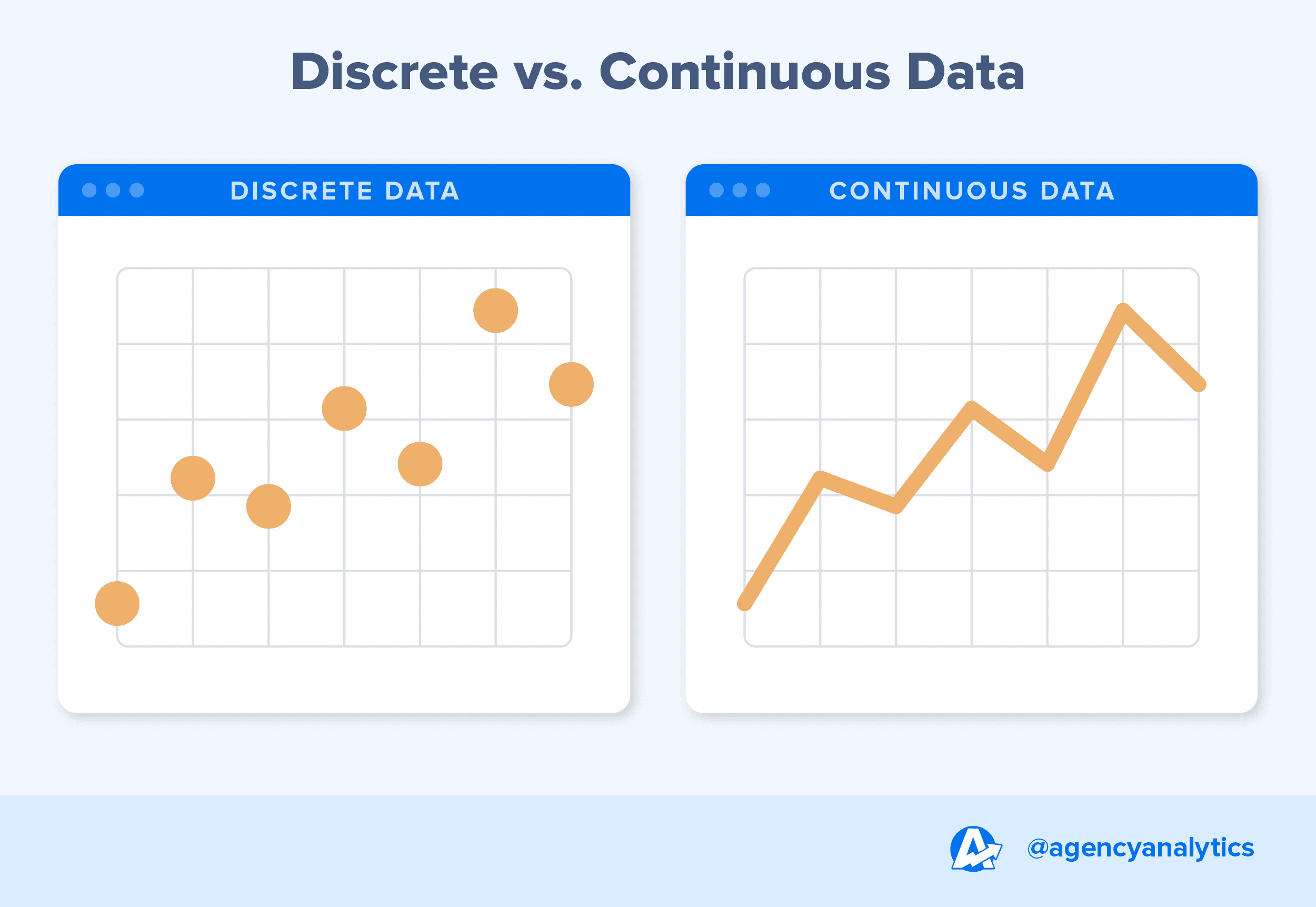
Datos discretos vs datos continuos. Link

Los datos pueden clasificarse en continuos o discretos. Los valores continuos pueden tomar cualquier número dentro de un rango, como la altura de una persona, ya que pueden existir valores intermedios con una precisión arbitraria. En contraste, los valores discretos solo pueden asumir ciertos valores específicos, como la cantidad de páginas de un libro, donde no existen valores intermedios entre un número entero y otro.

2. Estrategias para la selección y validación de datos

Los datos son un elemento esencial en los algoritmos de aprendizaje automático. Sin una selección adecuada, es posible obtener relaciones no significativas o incluso perjudiciales.

No todos los datos o métricas son útiles, por lo que es fundamental ajustarse al problema, asegurar la coherencia dentro de la misma distribución y minimizar la presencia de valores atípicos. Una correcta selección de los datos permite desarrollar modelos más robustos. Para ello, se emplea la validación cruzada.

2.1. Validación cruzada

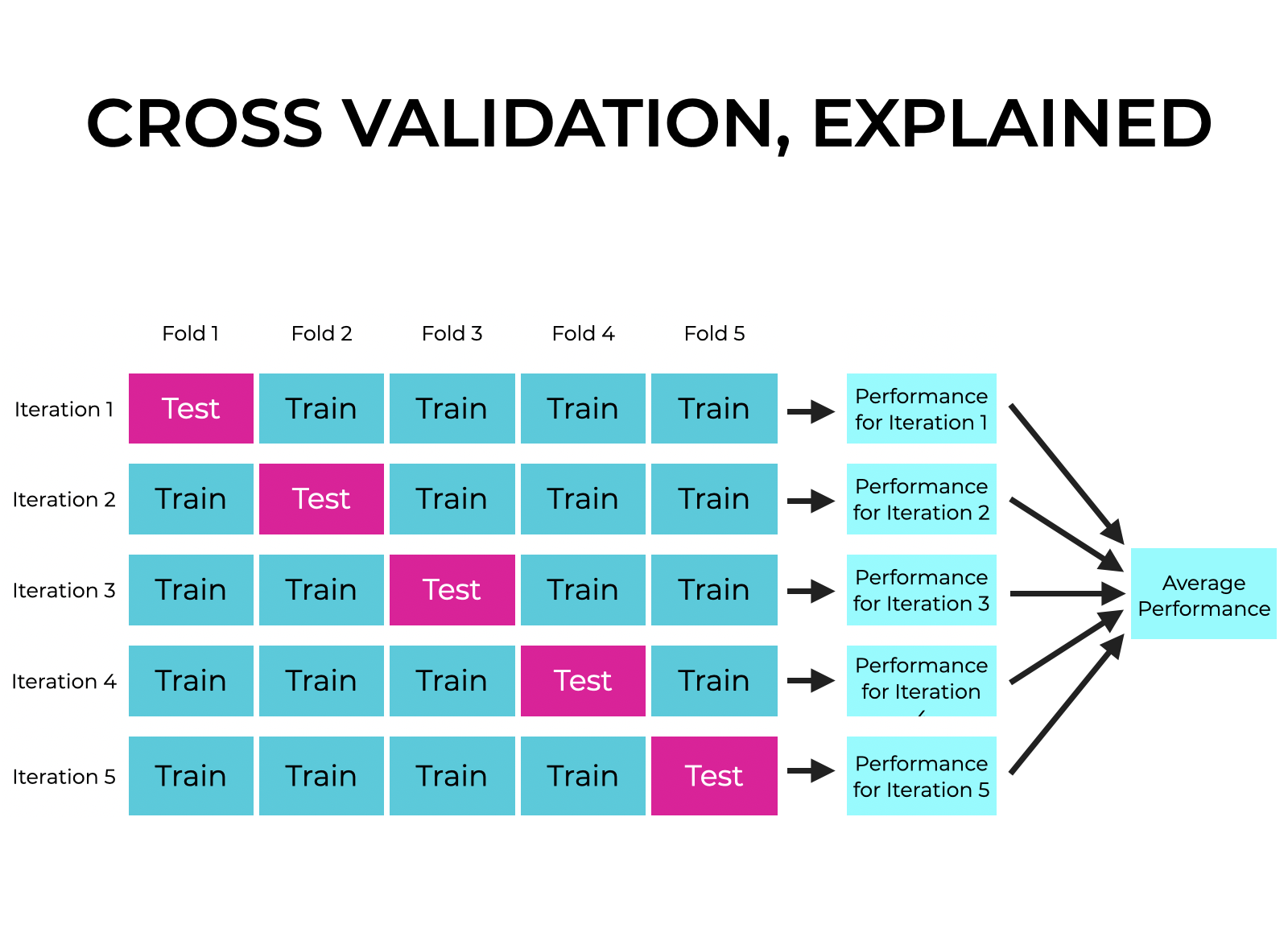
Esquema de funcionamiento de la validación cruzada. Link

La selección de muestras para el entrenamiento y validación de un modelo puede resultar compleja, ya que una elección inadecuada puede generar sesgos en el modelo.

Por ejemplo, en conjuntos de datos con dependencia temporal, como el tráfico de una red a lo largo del día, la distribución de las muestras en el conjunto de datos puede influir en el desempeño del modelo. Si los datos se registran en orden cronológico y las primeras muestras corresponden a la mañana, mientras que las últimas a la noche, seleccionar las primeras muestras para entrenamiento y las últimas para prueba, podría generar un modelo que no capture correctamente patrones generales.

Para evitar este problema, se recomienda introducir aleatoriedad en la selección de las muestras y definir un porcentaje para cada partición del conjunto de datos.

nota

Es fundamental establecer una semilla aleatoria antes de cualquier proceso que requiera aleatorización, garantizando así la reproducibilidad de los resultados.

Por ejemplo, el siguiente código establece semillas para las bibliotecas más utilizadas en Python para aprendizaje automático y profundo, garantizando la reproducibilidad de los experimentos:

import random
import numpy as np
import tensorflow as tf
import torch
import sklearn.utils

# Valor de la semilla
SEED = 42

# Establecer semilla en Python (random)
random.seed(SEED)

# Establecer semilla en NumPy
np.random.seed(SEED)

# Establecer semilla en TensorFlow
tf.random.set_seed(SEED)

# Establecer semilla en PyTorch
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)  # Para GPUs
torch.cuda.manual_seed_all(SEED)  # Para múltiples GPUs
torch.backends.cudnn.deterministic = True  # Para reproducibilidad en CUDA
torch.backends.cudnn.benchmark = False

# Establecer semilla en Scikit-learn
sklearn.utils.check_random_state(SEED)

Otra estrategia para la selección de datos es la validación cruzada, la cual consiste en dividir el conjunto de datos en múltiples partes y realizar iteraciones en las que se alternan los subconjuntos destinados a entrenamiento y prueba. Si se opta por una validación cruzada de 5 particiones (5-fold cross-validation), el modelo se entrena y evalúa cinco veces, cada vez utilizando un subconjunto distinto para prueba y los demás para entrenamiento. Posteriormente, los resultados obtenidos en cada iteración se promedian para obtener una evaluación más robusta del modelo.

El proceso de validación cruzada se basa en la partición de los datos en subconjuntos denominados folds. En cada iteración, se entrena el modelo con algunos folds y se evalúa con el fold restante. Este procedimiento se repite hasta que cada fold haya sido utilizado tanto para entrenamiento como para prueba. Finalmente, los resultados se promedian utilizando métricas como la precisión o el error del modelo.

Una ventaja de la validación cruzada es la reducción del problema conocido como data leakage, que ocurre cuando características utilizadas en el entrenamiento también están presentes en la fase de prueba, generando una evaluación artificialmente optimista del modelo.

3. Conceptos de estadística

3.1. Distribuciones

Antes de realizar predicciones, es fundamental recopilar datos. En muchas ocasiones, esta recopilación genera histogramas, que permiten visualizar la distribución de los datos.

Un histograma se compone de dos ejes principales: el eje x, donde se representan los datos agrupados en categorías, y el eje y, que indica la frecuencia de cada categoría, es decir, el número de muestras que pertenecen a cada grupo. Las divisiones en el eje x para agrupar los datos en rangos similares se conocen como bins o contenedores.

El uso de histogramas facilita la identificación de tendencias en los datos. En casos donde los valores pueden solaparse, los bins ayudan a agrupar puntos de datos dentro de un intervalo definido. De este modo, se generan distribuciones que permiten analizar el comportamiento de los datos.

nota

La elección del número de bins es crucial, ya que debe reflejar correctamente la distribución de los datos. Este tipo de histogramas resulta especialmente útil en algoritmos como Naïve Bayes, donde se generan distribuciones de probabilidad en cada iteración, permitiendo obtener valores como medias e intervalos de confianza.

El conjunto completo de datos recopilados se denomina población y se representa con la letra $N$. Un subconjunto de la población se denomina muestra y se representa con la letra $n$.

La probabilidad de que un dato pertenezca a una determinada parte del histograma se calcula dividiendo el número de muestras en esa sección entre el número total de muestras en la población.

nota

La confianza en los resultados depende del tamaño de la muestra: cuanto mayor sea el número de muestras, mayor será la confianza en la estimación. Donde la confianza representa el grado de incertidumbre asociado a una probabilidad.

3.2. Características de la probabilidad

La probabilidad está normalizada en un rango de 0 a 1, donde 0 indica imposibilidad y 1 certeza absoluta. Cuando todos los resultados posibles tienen la misma probabilidad, se habla de equiprobabilidad. Además, la suma de todas las probabilidades en un sistema debe ser 1.

Cuando el número de datos disponibles es insuficiente, las estimaciones de probabilidad pueden no ser precisas. No obstante, recopilar más datos puede resultar costoso en términos de tiempo, esfuerzo y dinero. Para mitigar esta limitación, se emplean distribuciones de probabilidad, que pueden ser discretas (cuando los datos toman valores específicos y finitos) o continuas (cuando los datos pueden tomar cualquier valor dentro de un rango determinado).

A continuación, se presentan algunas de las distribuciones más comunes.

3.2.1. Distribución binomial (discreta)

Cuando se trabaja con datos discretos y se requiere calcular probabilidades en eventos independientes con solo dos posibles resultados, éxito o fracaso (representados por 1 y 0, respectivamente), se trata de un problema binario.

Para modelar este tipo de situaciones, se utiliza la distribución binomial, que permite calcular la probabilidad de obtener una determinada cantidad de éxitos en una secuencia de ensayos independientes. La distribución binomial se expresa mediante la siguiente fórmula:

$$P(X = k | n, p) = \binom{n}{k} \cdot p^k \cdot (1 - p)^{n - k},$$

donde:

• $X$ representa el número de éxitos en los ensayos.
• $n$ es el número total de ensayos.
• $p$ es la probabilidad de éxito en un único ensayo.
• $k$ es el número de éxitos deseados.
• $\binom{n}{k}$ es el coeficiente binomial, que calcula de cuántas formas se pueden obtener $k$ éxitos en $n$ ensayos, sin importar el orden. Se calcula mediante la siguiente fórmula:

$$\binom{n}{k} = \frac{n!}{k! \cdot (n-k)!}.$$

Esta distribución es útil en situaciones donde se realizan múltiples intentos independientes de un mismo experimento y se desea conocer la probabilidad de obtener un número específico de éxitos.

Ejemplo

Supongamos que se lanza una moneda equilibrada (equiprobable, la probabilidad de tener cara es la misa que de tener cruz) 5 veces y se quiere calcular la probabilidad de obtener exactamente 3 caras.

Se definen los parámetros:

• $n = 5$ (número total de lanzamientos).
• $p = 0.5$ (probabilidad de obtener cara en un solo lanzamiento).
• $k = 3$ (número de caras que se desean obtener).

Aplicando la fórmula de la distribución binomial:

$$P(X = 3 | n=5, p=0.5) = \binom{5}{3} \cdot (0.5)^3 \cdot (1 - 0.5)^{5 - 3}$$

Calculamos el coeficiente binomial:

$$\binom{5}{3} = \frac{5!}{3! \cdot (5-3)!} = \frac{5!}{3! \cdot 2!} = 10$$

Sustituyendo en la ecuación:

$$P(X = 3) = 10 \cdot (0.5)^3 \cdot (0.5)^2 = 0.3125$$

Por lo tanto, la probabilidad de obtener exactamente 3 caras en 5 lanzamientos de una moneda equilibrada es del 31.25%.

3.2.2. Distribución de Poisson (discreta)

La distribución de Poisson se utiliza para modelar la probabilidad de que ocurra un número determinado de eventos en un intervalo de tiempo o espacio, siempre que los eventos ocurran de manera independiente y a una tasa promedio constante. Algunos ejemplos de aplicación incluyen: el número de llamadas recibidas en una central telefónica durante una hora, el número de accidentes en una intersección en un día, o la cantidad de errores tipográficos en una página de texto.

La distribución de Poisson se expresa mediante la siguiente fórmula:

$$P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!},$$

donde:

• $X$ es el número de eventos que ocurren en un intervalo específico.
• $\lambda$ es el número promedio de eventos en dicho intervalo.
• $k$ es el número de eventos cuya probabilidad se desea calcular.
• $e$ es la base del logaritmo natural.

Esta distribución es especialmente útil cuando se estudian eventos raros o poco frecuentes en un período de tiempo determinado.

Ejemplo

Supongamos que una central telefónica recibe en promedio 10 llamadas por hora y se desea calcular la probabilidad de que en una hora lleguen exactamente 7 llamadas.

Se definen los parámetros:

• $\lambda = 10$ (promedio de llamadas por hora).
• $k = 7$ (número específico de llamadas que se desea calcular).

Aplicamos la fórmula de la distribución de Poisson:

$$P(X = 7) = \frac{10^7 e^{-10}}{7!} \approx 0.0902$$

Por lo tanto, la probabilidad de recibir exactamente 7 llamadas en una hora es del 9.02%.

3.2.3. Distribución Normal o Gaussiana (continua)

La distribución normal, también denominada distribución gaussiana, se representa mediante una curva en forma de campana. En esta distribución, el eje $y$ indica la verosimilitud (likelihood) de observar un determinado valor en el eje $x$.

Verosimilitud vs. Probabilidad

Aunque son conceptos relacionados, la verosimilitud y la probabilidad tienen diferencias clave:

• Probabilidad: Representa la posibilidad de que ocurra un evento dado un modelo y sus parámetros. Se expresa como $P(D|\theta)$, donde $D$ son los datos y $\theta$ los parámetros del modelo. Responde a la pregunta: Dado que los parámetros del modelo son conocidos, ¿qué tan probable es observar ciertos datos?
• Verosimilitud: Mide qué tan bien un conjunto de parámetros explica un conjunto de datos observados. Se denota como $L(\theta | D)$ y representa la plausibilidad de los parámetros $\theta$ dados los datos $D$. Responde a la pregunta: Dado que los datos han sido observados, ¿qué tan plausible es que provengan de un modelo con ciertos parámetros?

Mientras que la probabilidad se emplea para predecir eventos futuros basándose en un modelo conocido, la verosimilitud se usa para evaluar qué tan bien un modelo con ciertos parámetros explica los datos observados. Para obtener probabilidades a partir de la verosimilitud, se puede utilizar el Teorema de Bayes.

La distribución normal es simétrica respecto a su media ($\mu$), lo que implica que el valor más verosímil es precisamente la media. La forma de la curva normal está determinada por dos parámetros: la media ($\mu$) y la desviación típica ($\sigma$).

• Una curva alta y estrecha indica que los datos están más concentrados alrededor de la media, lo que corresponde a una baja varianza.
• Una curva baja y ancha sugiere una mayor dispersión de los datos, es decir, mayor varianza.

La desviación típica ($\sigma$) mide la dispersión de los datos respecto a la media, mientras que la varianza ($\sigma^2$) es el cuadrado de la desviación típica. La varianza se puede calcular de las siguientes dos maneras:

• Varianza muestral:

  $$s^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}.$$

• Varianza poblacional:

  $$\sigma^2 = \frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}.$$

Donde:

• $x_i$ son los valores de la muestra o población.
• $\bar{x}$ es la media muestral.
• $\mu$ es la media poblacional.
• $n$ es el tamaño de la muestra.
• $N$ es el tamaño de la población.

La distribución normal es fundamental en estadística y aprendizaje automático debido a su presencia en numerosos fenómenos naturales y conjuntos de datos del mundo real.

3.2.3.1. Función de Densidad de Probabilidad

La función de densidad de probabilidad (Probability Distribution Function, PDF) de la distribución normal se define como:

$$f(X|\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x_i - \mu)^2}{2\sigma^2}}.$$

En las distribuciones continuas, el cálculo de probabilidades requiere la integración de la función de densidad de probabilidad (PDF). Esta integración permite obtener el área bajo la curva entre dos puntos, lo que representa la probabilidad acumulada en dicho intervalo. Dado que el área total bajo la curva es igual a 1, el área acumulada hasta la media en una distribución normal es de 0.5.

Es importante destacar que la probabilidad exacta en un único punto es igual a 0. Esto se debe a que, gráficamente, un punto no tiene ancho y, por lo tanto, no contribuye con área bajo la curva. En consecuencia, solo es posible calcular probabilidades en intervalos.

La función de distribución acumulada (Cumulative Distribution Function, CDF) expresa la probabilidad acumulada hasta un determinado valor. Matemáticamente, representa el área bajo la curva de la función de densidad desde $-\infty$ hasta dicho punto.

3.2.3.2. Propiedades de la Función de Densidad de Probabilidad

Sea $F$ la función de distribución acumulada (CDF) y $\mathbb{R}$ el conjunto de números reales, entonces se cumple que $F: \mathbb{R} \to [0,1]$, lo que significa que el rango de valores de la función de distribución está comprendido entre 0 y 1.

nota

Se usa mayúscula para $F(x)$ porque se refiere a la función matemática que mapea los valores de la variable aleatoria $X$ a la probabilidad acumulada, distinguiéndola de la función de densidad de probabilidad que se representa en minúscula, como $f(x)$.

Algunas de sus propiedades fundamentales son:

• $F(x) = P(A_x) = P(X \leq x)$, donde $A_x$ representa el evento $X \leq x$.
• $P(X \leq x) = F(x)$, lo que corresponde a la función de distribución acumulada (CDF).
• $P(X > x) = 1 - P(X \leq x) = 1 - F(x)$, es decir, la probabilidad complementaria a $P(X \leq x)$.
• $P(a < X \leq b) = F(b) - F(a)$, para calcular la probabilidad de que $X$ esté entre dos valores $a$ y $b$.
• $P(X \geq a) = P(X > a) + P(X = a)$, una forma de descomponer la probabilidad de que $X$ sea mayor o igual que $a$.
• $P(X = a) = F(a) - \lim\_{h \to 0^+} F(a - h) = F(a) - P(X \leq a)$, que calcula la probabilidad de que $X$ tome el valor $a$.

Estas propiedades permiten calcular probabilidades acumuladas y facilitan el análisis de distribuciones de probabilidad continuas.

Ejemplo

Se desea calcular la probabilidad de que un valor se encuentre en el intervalo $[142.5, 155.7]$ en una distribución normal $N(\mu=155.7, \sigma=6.6)$.

La probabilidad se obtiene a partir de la función de distribución acumulada (CDF):

$P(a < X \leq b) = P(142.5 < X \leq 155.7) = F(155.7) - F(142.5)$

$P(X \leq 155.7) - P(X \leq 142.5) \approx 0.5 - 0.02275 \approx 0.4772$

Implementación en Python:

from statistics import NormalDist

# Se calcula la función de distribución acumulada (CDF) en los puntos de interés
cdf_p1 = NormalDist(155.7, 6.6).cdf(155.7)
# cdf_p1 = 0.5, debido a la simetría de la distribución normal

cdf_p2 = NormalDist(155.7, 6.6).cdf(142.5)
# cdf_p2 ≈ 0.02275

# Se obtiene la probabilidad del intervalo restando las probabilidades acumuladas
diff = cdf_p1 - cdf_p2
# diff ≈ 0.4772 = 47.72%

Por lo tanto, la probabilidad de que un valor de esta distribución normal se encuentre en el intervalo $[142.5, 155.7]$ es aproximadamente del 47.72%.

3.2.4. Distribución Exponencial (continua)

La distribución exponencial se emplea para modelar el tiempo transcurrido entre eventos en un proceso de Poisson, donde los eventos ocurren de manera independiente y con una tasa constante. Se utiliza en el análisis de tiempos de espera, confiabilidad de sistemas y modelado de fallos en ingeniería.

La función de densidad de probabilidad (PDF) está definida como:

$$f(x; \lambda) = \lambda e^{-\lambda x}, \quad x \geq 0, \, \lambda > 0,$$

donde $\lambda$ indica la frecuencia con la que ocurren los eventos.

La función de distribución acumulada (CDF) se expresa como:

$$F(x) = 1 - e^{-\lambda x}, \quad x \geq 0.$$

La media de la distribución exponencial equivale a la esperanza matemática $E[X]$.

nota

La esperanza matemática, denotada como $E[X]$, es lo que comúnmente llamamos la media o el valor esperado de una variable aleatoria. Sin embargo, la interpretación de la esperanza matemática puede variar dependiendo del tipo de variable aleatoria y el contexto en el que se utilice.

Para una variable aleatoria discreta $X$, cuya función de masa de probabilidad es $P(X = x_i)$, la esperanza matemática se calcula mediante la siguiente fórmula:

$$E[X] = \sum_{i} x_i \cdot P(X = x_i)$$

En este caso, el valor esperado se obtiene sumando el producto de cada valor posible de $X$ y su probabilidad correspondiente.

Para una variable aleatoria continua $X$, cuya función de densidad de probabilidad es $f(x)$, la esperanza matemática se calcula utilizando la integral de la siguiente manera:

$$E[X] = \int_{-\infty}^{\infty} x \cdot f(x) \,dx$$

Aquí, el valor esperado se obtiene integrando el producto de cada valor de $X$ y su densidad de probabilidad asociada.

En teoría de probabilidad, la esperanza matemática se considera la media "teórica" de la distribución. En distribuciones simétricas con un único pico, como la distribución normal, la esperanza matemática coincide con el centro de la distribución. Sin embargo, en distribuciones asimétricas, la esperanza matemática puede no coincidir con la mediana o la moda. Por ejemplo, en una distribución sesgada a la derecha, como la distribución exponencial, la esperanza matemática es mayor que la mediana, lo que indica que los valores más altos de la variable aleatoria tienen una probabilidad significativa de ocurrir.

En la distribución exponencial, se obtiene:

$$\mu = E[X] = \frac{1}{\lambda}.$$

La varianza se expresa como:

$$\sigma^2 = \frac{1}{\lambda^2}.$$

3.2.5. Distribución Uniforme (continua)

La distribución uniforme se caracteriza porque todos los valores dentro de un intervalo $[a, b]$ tienen la misma probabilidad de ocurrir. Se emplea en la generación de números aleatorios, simulaciones y situaciones en las que no hay preferencia por ningún valor específico dentro de un rango determinado.

La función de densidad de probabilidad (PDF) para una distribución uniforme continua es:

$$f(x) = \begin{cases} \frac{1}{b-a}, & a \leq x \leq b \\ 0, & \text{en otro caso} \end{cases}$$

La función de distribución acumulada (CDF) está dada por:

$$F(x) = \begin{cases} 0, & x < a \\ \frac{x-a}{b-a}, & a \leq x \leq b \\ 1, & x > b \end{cases}$$

La media de la distribución uniforme es:

$$\mu = E[X] = \frac{a + b}{2}.$$

Y su varianza se expresa como:

$$\sigma^2 = \frac{(b-a)^2}{12}.$$

¿De dónde sale el 12 de la varianza de la distribución uniforme?

La varianza de una variable aleatoria continua $X$ se define como:

$$\text{Var}(X) = E[X^2] - (E[X])^2.$$

Para una distribución uniforme continua $U(a, b)$, la esperanza, la cual coincide con la media, se obtiene con la fórmula:

$$E[X] = \frac{a+b}{2}.$$

Por tanto, el cálculo de $E[X^2]$ se calcula como:

$$E[X^2] = \int_a^b x^2 \cdot f(x) \, dx = \int_a^b x^2 \cdot \frac{1}{b-a} \, dx.$$

Resolviendo la integral:

$$E[X^2] = \frac{1}{b-a} \int_a^b x^2 \, dx = \frac{1}{b-a} \cdot \left[ \frac{x^3}{3} \right]_{a}^{b}.$$

Evaluando de $a$ a $b$:

$$E[X^2] = \frac{1}{b-a} \left[ \frac{b^3}{3} - \frac{a^3}{3} \right] = \frac{b^3 - a^3}{3(b-a)}.$$

Ahora, usando la fórmula de la varianza y sustituyendo los valores obtenemos:

$$\text{Var}(X) = E[X^2] - (E[X])^2 = \frac{b^3 - a^3}{3(b-a)} - \left(\frac{a+b}{2} \right)^2.$$

Aplicando las identidades algebraicas siguientes:

$$(a+b)^{2}=a^2+b^2+2ab,$$$$b^3 - a^3 = (b-a)(b^2 + ab + a^2),$$

Finalmente, después de desarrollar la expresión y simplificar, se obtiene la expresión:

$$\text{Var}(X) = \frac{(b-a)^2}{12}$$

3.3. Evaluación del error

Los modelos de aprendizaje automático requieren datos de entrenamiento para establecer relaciones entre las variables y construir una función que se aproxime a la distribución de los datos. Un aspecto fundamental en este proceso es la evaluación del desempeño del modelo, lo cual se realiza mediante métricas estadísticas.

3.3.1. Suma de los Cuadrados de los Residuales (SSR)

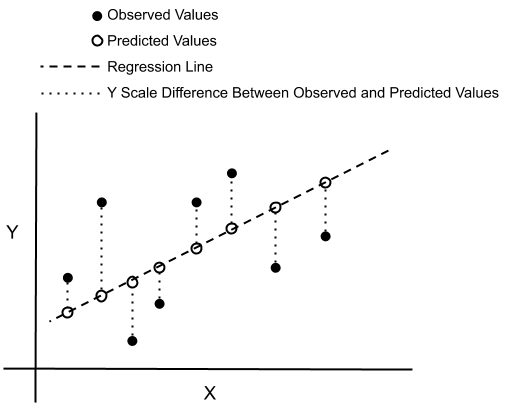
Ejemplo de SSR. Link

La Suma de los Cuadrados de los Residuales (Sum Square Residuals, SSR) mide la diferencia entre las predicciones del modelo y los valores reales. Se calcula sumando el cuadrado de estas diferencias, lo que permite evaluar qué tan buena es la predicción del modelo. Un valor bajo de SSR indica un mejor ajuste.

Matemáticamente, la SSR se expresa como:

$$SSR = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2,$$

donde:

• $y_i$ es el valor real.
• $\hat{y}_i$ es el valor estimado por el modelo.
• $n$ es el número total de observaciones.

Sin embargo, la SSR depende del número de datos, lo que puede dificultar la comparación entre modelos. Para abordar este problema, se emplea el Error Cuadrático Medio (MSE).

3.3.2. Error Cuadrático Medio (MSE)

El Error Cuadrático Medio (MSE) se obtiene dividiendo la SSR entre el número total de muestras. Su objetivo es promediar la magnitud del error para normalizarlo con respecto al tamaño del conjunto de datos. Se define como:

$$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2.$$

A pesar de que el MSE proporciona una medida más interpretable del error, sigue dependiendo de la escala de los datos. Para eliminar esta dependencia, se emplea el Coeficiente de Determinación ($R^2$).

3.3.3. Coeficiente de Determinación

El Coeficiente de Determinación ($R^2$) mide la capacidad del modelo para replicar los resultados observados y la proporción de variabilidad explicada por el modelo en comparación con la media de los datos. Se expresa como:

$$R^2 = 1 - \frac{\text{SSR}}{SST} = 1 - \frac{\text{SSR}(\text{respecto al modelo})}{\text{SSR}(\text{respecto a la media})}$$

donde:

• $\text{SST}$ es la Suma Total de los Cuadrados, que representa la variabilidad total de los datos en torno a la media.

El coeficiente $R^2$ varía entre 0 y 1, donde un valor cercano a 1 indica que el modelo explica bien la varianza de los datos, lo que sugiere un buen ajuste. En cambio, un valor cercano a 0 sugiere que el modelo apenas mejora la predicción en comparación con la media. Si $R^2$ es negativo, el modelo tiene un mal ajuste y predice peor que la media.

El coeficiente $R^2$ se emplea en problemas de regresión sobre datos continuos.

nota

El coeficiente $R^2$ equivale al cuadrado del coeficiente de correlación de Pearson solo en el caso de la regresión lineal simple.

3.3.4. Coeficiente de Correlación de Pearson

Ejemplo de la correlación para una nuve de puntos. Link

El Coeficiente de Correlación de Pearson mide la relación lineal entre dos variables cuantitativas y continuas. Se define como:

$$r = \frac{\text{cov}(X,Y)}{\sigma_X \sigma_Y}$$

donde:

• $\text{cov}(X,Y)$ es la covarianza entre las variables $X$ e $Y$.
• $\sigma_X$ y $\sigma_Y$ son las desviaciones típicas de $X$ e $Y$, respectivamente.

La covarianza indica la relación entre dos variables:

• Si la covarianza es positiva, un aumento en $X$ se asocia con un aumento en $Y$ (relación directa).
• Si la covarianza es negativa, un aumento en $X$ se asocia con una disminución en $Y$ (relación inversa).
• Una covarianza cercana a 0 sugiere que no existe relación lineal entre las variables.

Dado que la covarianza depende de la escala de las variables, se normaliza mediante el coeficiente de correlación de Pearson, que toma valores entre -1 y 1, donde:

• 1: correlación positiva perfecta.
• -1: correlación negativa perfecta.
• 0: ausencia de correlación lineal.

Este coeficiente permite evaluar la intensidad y dirección de la relación lineal entre las variables sin depender de su escala.

4. Modelos clásicos

Una vez comprendido el concepto de modelo de aprendizaje automático, donde se utilizan datos para modelar su distribución, analizar relaciones y extraer conocimiento, es posible aplicar estos modelos para realizar tareas como clasificación de nuevos datos, predicción de valores y otras aplicaciones. A continuación, se presentan algunos de los métodos más utilizados.

tip

A pesar del auge de los modelos de lenguaje basados en arquitecturas de aprendizaje profundo (Deep Learning), su aplicación sigue siendo limitada en ciertos contextos debido a la gran cantidad de datos y capacidad de cómputo que requieren, así como a la necesidad de explicabilidad en sectores específicos. Por ello, los métodos tradicionales siguen desempeñando un papel fundamental, especialmente en el análisis de datos tabulares, los cuales representan la mayoría de los datos empresariales.

Es recomendable iniciar con modelos más sencillos para comprender los resultados y evaluar su utilidad en función de los objetivos del análisis. A partir de esta base, y considerando factores como el tiempo y los recursos disponibles, se puede optar por soluciones más complejas que ofrezcan un mayor retorno de inversión (ROI).

4.1. Regresión lineal

4.2. Descenso del gradiente

4.3. Regresión logística

4.4. Naive Bayes

4.5. Árboles de Decisión

4.5.X. Random Forest

Random Forest es una técnica de ensamblado basada en árboles de decisión que mejora la capacidad de generalización de estos últimos. Aunque los árboles de decisión clásicos son fácilmente interpretables y eficientes en el ajuste a los datos de entrenamiento, presentan una alta varianza que los hace poco robustos frente a nuevas muestras. Random Forest soluciona esta limitación mediante un enfoque basado en el aprendizaje conjunto de múltiples árboles de decisión.

El proceso de construcción de un modelo Random Forest se compone de tres etapas fundamentales:

1. Generación de conjuntos de entrenamiento mediante bootstrap: A partir del conjunto de datos original, se crean múltiples subconjuntos de entrenamiento mediante muestreo aleatorio con reemplazo. Este procedimiento se conoce como bootstrap sampling. Como consecuencia, algunas observaciones pueden repetirse dentro de un subconjunto, mientras que otras no serán seleccionadas.

2. Construcción de árboles de decisión: Cada subconjunto generado se utiliza para entrenar un árbol de decisión independiente. A diferencia del procedimiento habitual, en cada división del árbol se selecciona aleatoriamente un subconjunto de características (features) en lugar de utilizar todas. Esta estrategia introduce diversidad entre los árboles y reduce la correlación entre ellos, lo que mejora el rendimiento general del modelo.

3. Agregación de predicciones (bagging): El término bagging (de bootstrap aggregating) hace referencia a la combinación de múltiples modelos entrenados sobre diferentes subconjuntos de datos. En Random Forest, esto se implementa promediando (para regresión) o votando (para clasificación) las predicciones generadas por cada árbol.

Durante el entrenamiento, algunas muestras no se utilizan en la construcción de un árbol determinado. Estas observaciones, conocidas como out-of-bag samples, se emplean para evaluar el rendimiento del modelo de manera interna, sin necesidad de un conjunto de validación adicional. Al calcular el porcentaje de muestras out-of-bag clasificadas incorrectamente por el conjunto de árboles, se obtiene el llamado out-of-bag error, que actúa como una estimación fiable del error de generalización.

Por último, el número de características consideradas en cada división puede ajustarse como hiperparámetro del modelo. Este control permite optimizar el equilibrio entre sesgo y varianza, mejorando la precisión y robustez del Random Forest frente a los árboles de decisión individuales.

4.6. Máquina de Vectores de Soporte

5. Algoritmos de agrupación

5.1. Tipos de algoritmos de agrupación

5.1.1. Métodos basados en particiones

5.1.2. Métodos basados en jerarquías

5.1.3. Métodos basados en densidad

5.1.4. Métodos basados en modelos (p.ej. GMM)

5.1.5. Métodos basados en grafos (p.ej. Spectral)

5.2. Mecanismos en la elección de grupos

6. Métodos de comparación de modelos

6.1. Clasificación

6.1.1. Matrices de confusión

6.2. Regresión

7. Métodos para la reducción de la dimensionalidad

7.1. PCA

7.2. T-SNE

7.3. UMAP

7.4. Auto Encoders

8. Métodos para la imputación de datos

La imputación de datos es una técnica fundamental en la preparación de datos, especialmente cuando se enfrentan valores faltantes en un conjunto. Dependiendo del tipo de variable (numérica o categórica), se aplican diferentes estrategias para completar los valores ausentes de manera coherente y eficiente.

8.1. Imputación simple

Para variables numéricas, se emplean habitualmente medidas de tendencia central como la media o la mediana. No obstante, la mediana es preferida en contextos reales debido a su mayor robustez frente a valores atípicos o fuera de distribución. La decisión entre usar media o mediana puede fundamentarse en un análisis estadístico preliminar, como el estudio de la función de distribución acumulada (CDF) y el rango intercuartílico (IQR), que corresponde a la diferencia entre el percentil 75 y el percentil 25. Esta evaluación permite identificar valores anómalos y decidir si deben eliminarse o si la imputación debe ajustarse a una medida más robusta como la mediana.

Para variables categóricas, la imputación más común se realiza mediante la moda, es decir, el valor más frecuente en la columna correspondiente. Cabe destacar que estas imputaciones se aplican por columna, es decir, por cada característica (feature) del conjunto de datos.

8.2. Imputación basada en vecinos

Una estrategia más avanzada es el uso de métodos basados en los vecinos más cercanos, como el algoritmo k-Nearest Neighbors (k-NN). Este enfoque consiste en identificar, para una muestra con valores faltantes, las muestras más similares (vecinas) utilizando métricas de distancia, como la distancia euclidiana. Una vez determinadas las k muestras más cercanas, el valor faltante se imputa en función de las características de esas vecinas, por ejemplo, mediante la media, la mediana o la moda de los valores presentes en ese grupo. Esta técnica permite imputar valores de forma contextualizada, mejorando la precisión respecto a métodos globales.

8.3. Imputación con modelos predictivos

8.3.1. MissForest

Un enfoque aún más sofisticado es MissForest, que emplea algoritmos de aprendizaje automático como Random Forest para imputar valores faltantes. El proceso consiste en:

1. Realizar una imputación inicial de los valores faltantes utilizando técnicas simples (media, mediana o moda según el tipo de variable).
2. Entrenar un modelo Random Forest con las características completas para predecir los valores ausentes de cada característica incompleta.
3. Actualizar los valores imputados con las predicciones obtenidas.
4. Repetir iterativamente el proceso hasta que se alcanza la convergencia o un número máximo de iteraciones.

MissForest es especialmente útil en contextos donde las relaciones entre variables son complejas y no lineales, ofreciendo un balance entre precisión y robustez.

En resumen, la selección del método de imputación más adecuado depende de la naturaleza de los datos, del patrón de ausencia y del nivel de precisión requerido en el análisis posterior.