Deep Learning

Bibliografía

1. Introducción al aprendizaje profundo

Antes de abordar el campo del aprendizaje profundo o Deep Learning, es fundamental comprender un concepto esencial que, aunque pueda parecer evidente, no siempre resulta fácil de definir: la inteligencia. Esta puede entenderse como la capacidad de procesar información y emplearla en la toma de decisiones futuras. A partir de esta noción surge la Inteligencia Artificial (IA), disciplina cuyo objetivo es desarrollar técnicas y algoritmos que permitan a las máquinas emular ciertos comportamientos humanos. En términos generales, la IA busca que los sistemas puedan utilizar la información disponible para realizar predicciones, adaptarse a distintos contextos y resolver problemas de manera autónoma.

Dentro de la IA se encuentra un subcampo crucial: el aprendizaje automático o Machine Learning. Su propósito es permitir que un ordenador aprenda de la experiencia sin necesidad de recibir instrucciones explícitas. En lugar de programar paso a paso cada acción, se diseñan algoritmos capaces de identificar patrones en los datos, de modo que el sistema mejore su rendimiento de forma automática a medida que acumula ejemplos. Este enfoque representa un cambio significativo respecto a la programación tradicional, ya que el sistema aprende a generalizar a partir de los datos, en lugar de ejecutar reglas predefinidas.

Un nivel más especializado es el Deep Learning, que utiliza redes neuronales artificiales para extraer patrones complejos a partir de datos sin procesar. Estas redes, inspiradas en la estructura y funcionamiento del cerebro humano, aprenden representaciones jerárquicas de la información, lo que les permite captar relaciones complejas entre variables. Gracias a esta capacidad, el Deep Learning resulta especialmente eficaz en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural, el análisis de audio y otros problemas que involucran grandes volúmenes de datos no estructurados.

1.1. Predicción de precios de viviendas mediante regresión lineal

Para ilustrar estos conceptos, consideremos un ejemplo sencillo: estimar el precio de una vivienda. Si representamos gráficamente el tamaño de la casa frente a su precio, se observa generalmente una tendencia positiva: a mayor tamaño, mayor precio. Un modelo matemático básico para capturar esta relación es la regresión lineal, que ajusta una recta a los datos. Sin embargo, esta solución presenta limitaciones: por ejemplo, una línea puede asignar valores negativos a viviendas muy pequeñas, lo cual no tiene sentido. Para corregirlo, se introducen funciones que restringen los resultados a un rango de valores válidos.

Este proceso se puede entender mediante el funcionamiento de una neurona o perceptrón. La neurona recibe como entrada el tamaño de la vivienda, realiza un cálculo lineal a partir de ejemplos recopilados y aplica una función que descarta valores inválidos, generando como salida una estimación coherente del precio. No obstante, el valor de una vivienda depende de múltiples factores adicionales, como el número de dormitorios, la ubicación o la calidad del vecindario. Incorporar varias características complica el modelo, ya que se incrementan las dimensiones de los datos, y la simple regresión lineal deja de ser suficiente. En estos casos, es necesario combinar múltiples regresiones lineales organizadas en capas, formando arquitecturas más complejas.

En una arquitectura de Deep Learning, se distingue una capa de entrada, que recibe las características iniciales, una o varias capas ocultas, donde se combinan y transforman dichas características, y una capa de salida, que genera la predicción final.

1.2. Elementos esenciales de una neurona artificial

Cada neurona asigna un peso a cada característica, lo que refleja su importancia relativa en el resultado frente a las demás variables. Además, incorpora un sesgo, un valor adicional que permite ajustar la función de salida y proporciona mayor flexibilidad al modelo, modulando la propensión de la neurona a activarse o desactivarse según los datos de entrada. Tanto los pesos como el sesgo se inicializan de forma aleatoria y se ajustan progresivamente durante el proceso de entrenamiento, optimizando el rendimiento del modelo.

El resultado de cada neurona pasa posteriormente por una función de activación no lineal, un componente crucial que permite a la red capturar relaciones complejas que van más allá de las simples combinaciones lineales y definir un rango coherente para la salida.

1.3. Tipos de arquitecturas y datos

El Deep Learning se adapta a distintos tipos de problemas mediante arquitecturas especializadas, lo que permite extraer información más relevante de los datos y comprender mejor los patrones subyacentes. Entre las principales arquitecturas se encuentran:

Redes neuronales densas o totalmente conectadas, adecuadas para datos tabulares.
Redes convolucionales (CNN, Convolutional Neural Networks), diseñadas para analizar imágenes y vídeos mediante la detección de patrones espaciales.
Redes recurrentes (RNN, Recurrent Neural Networks) y sus variantes modernas, idóneas para procesar secuencias como texto, series temporales o audio.
Modelos multimodales, capaces de integrar simultáneamente información de diferentes fuentes, como texto, imágenes y sonido.

Al analizar los datos, es importante distinguir entre:

Datos estructurados, organizados en tablas con filas y columnas, típicos de bases de datos tradicionales. En estos casos, a menudo es suficiente aplicar algoritmos de aprendizaje automático más simples en lugar de recurrir a Deep Learning.
Datos no estructurados, como imágenes, grabaciones de voz o documentos de texto libre, que requieren arquitecturas más avanzadas para su procesamiento. El Deep Learning sobresale en estos contextos debido a su capacidad para interpretar y extraer patrones complejos de grandes volúmenes de información no estructurada.

1.4. Factores que impulsan su desarrollo

El auge del Deep Learning en la última década se explica por la confluencia de tres factores principales. En primer lugar, la disponibilidad masiva de datos, favorecida por la digitalización y la conectividad global, proporciona la materia prima necesaria para entrenar modelos complejos. En segundo lugar, los avances en hardware especializado, como GPUs y TPUs, permiten entrenar modelos de gran escala en tiempos razonables. Empresas como NVIDIA han desarrollado GPUs optimizadas para el cálculo matricial requerido en el aprendizaje profundo, complementadas con librerías como CUDA. Además, se observa una tendencia hacia arquitecturas diseñadas específicamente para inteligencia artificial, como NPU y TPUs, integradas en dispositivos móviles y embebidos, que permiten ejecutar modelos de manera eficiente, privada y sin conexión a Internet.

El tercer factor son las mejoras en algoritmos y técnicas de optimización, que han permitido abordar problemas antes inabordables. La combinación de estos factores ha democratizado el uso del Deep Learning, promoviendo la aparición de startups que liberan modelos de código abierto, parámetros de entrenamiento e incluso los datos utilizados, facilitando así la investigación y el desarrollo de nuevas aplicaciones basadas en inteligencia artificial.

2. Regresión lineal y logística

El entrenamiento de una neurona o de una red neuronal se fundamenta en dos procesos esenciales: la propagación hacia adelante (forward propagation) y la propagación hacia atrás (backpropagation).

La propagación hacia adelante consiste en calcular la predicción del modelo a partir de los datos de entrada. En este proceso, los datos ingresan por la capa de entrada y atraviesan las distintas capas de la red, generando una representación que permite al modelo estimar la salida.

Por su parte, la propagación hacia atrás se encarga de ajustar los parámetros internos del modelo (pesos y sesgos) con el objetivo de minimizar el error de predicción. Durante este proceso, los gradientes fluyen desde la salida hacia la entrada, permitiendo la actualización progresiva de los parámetros en cada iteración para mejorar la precisión del modelo.

Con estos mecanismos en mente, es útil analizar un caso clásico de aprendizaje automático: la clasificación binaria, que consiste en asignar a cada ejemplo una de dos posibles clases.

2.1. Detección de gatos en imágenes mediante regresión logística

Un ejemplo representativo de clasificación binaria se encuentra en la detección de objetos en imágenes, como identificar si una imagen contiene un gato. En este escenario, cada ejemplo se etiqueta de manera binaria, 1 si la imagen contiene un gato y 0 si no. Aunque este problema puede ampliarse a clasificación multiclase, para fines ilustrativos se considera únicamente la clasificación binaria.

Cada imagen se representa con dimensiones de 64×64 píxeles y formato RGB, generando tres matrices que corresponden a los canales de color rojo, verde y azul. Cada matriz tiene dimensiones 64×64, lo que da un total de valores por imagen de:

64 \times 64 \times 3 = 12288

Para introducir esta información en un modelo de red neuronal, se aplica la técnica de aplanamiento (flatten), que transforma las tres matrices en un único vector columna de dimensión $12288 × 1$ , manteniendo toda la información relevante de los píxeles.

Las etiquetas indican al modelo la clase correspondiente de cada ejemplo. Por ejemplo, una imagen denominada gato.png recibe la etiqueta 1, mientras que otra que no contenga un gato recibe 0. Dado que cada imagen está acompañada de su etiqueta, este escenario corresponde a lo que se denomina como aprendizaje supervisado.

Si se dispone de $M$ ejemplos, la matriz de características X tendrá dimensión (n, M), donde $n = 12288$ , y el vector de etiquetas Y tendrá dimensión (1, M), conteniendo únicamente valores binarios.

Para abordar este problema se utiliza la regresión logística, un algoritmo supervisado diseñado específicamente para tareas con etiquetas binarias (ceros y unos). Su funcionamiento es similar al de la regresión lineal, con la diferencia clave de que la salida se transforma mediante la función sigmoide, que restringe el resultado a un valor entre 0 y 1, interpretable como probabilidad y definida como

\sigma(z) = \frac{1}{1 + e^{-z}},

donde

z = w^T x + b.

En esta ecuación, $w$ representa los pesos, $b$ el sesgo y $x$ el vector de características de entrada. La predicción final del modelo se expresa como

\hat{y} = \sigma(w^T x + b),

donde $\hat{y}$ corresponde a la probabilidad de que la imagen pertenezca a la clase positiva, es decir, que efectivamente contenga un gato. Esta representación permite interpretar las salidas del modelo de forma probabilística y establecer umbrales para la clasificación binaria de manera consistente y flexible.

2.2. Función de pérdida y coste

El objetivo del modelo es ajustar los parámetros $w$ y $b$ de manera que las predicciones $\hat{y}$ se aproximen lo más posible a los valores reales $y$ . Para evaluar y guiar este ajuste se utilizan dos métricas fundamentales:

Función de pérdida, que cuantifica el error en un único ejemplo individual.
Función de coste, que representa el promedio de las pérdidas de todos los ejemplos del conjunto de entrenamiento.

En regresión logística, la función de pérdida utilizada es la función de pérdida logística o log-loss, definida como

\mathcal{L}(\hat{y}, y) = - \big( y \cdot \log(\hat{y}) + (1-y)\cdot \log(1-\hat{y}) \big).

Esta función penaliza de manera más adecuada los errores en problemas de clasificación binaria en comparación con el error cuadrático medio, que se define como

\text{MSE} = \frac{1}{M} \sum_{i=1}^{M} (\hat{y}^{(i)} - y^{(i)})^2.

La función de coste asociada a la regresión logística se obtiene como el promedio de las pérdidas de todos los ejemplos, representada como

J(w, b) = \frac{1}{M} \sum_{i=1}^{M} \mathcal{L}(\hat{y}^{(i)}, y^{(i)}).

Esta formulación basada en log-loss evita problemas de múltiples mínimos locales y garantiza una optimización más estable y eficiente en tareas de clasificación binaria, proporcionando gradientes más consistentes durante el entrenamiento.

2.3. Descenso del gradiente

El entrenamiento de un modelo de regresión logística tiene como objetivo encontrar los valores de $w$ y $b$ que minimicen la función de coste $J(w, b)$ . Para ello se emplea el descenso del gradiente, un algoritmo iterativo que ajusta los parámetros en la dirección que produce la mayor reducción del error.

Si recordamos, la función de coste en regresión logística se define como

J(w, b) = \frac{1}{M} \sum_{i=1}^{M} \mathcal{L}(\hat{y}^{(i)}, y^{(i)}) = -\frac{1}{M} \sum_{i=1}^{M} \Big[ y^{(i)} \log(\hat{y}^{(i)}) + (1-y^{(i)}) \log(1-\hat{y}^{(i)}) \Big],

donde $M$ es el número total de ejemplos, $\hat{y}^{(i)} = \sigma(w^T x^{(i)} + b)$ es la predicción para el ejemplo $i$ , $x^{(i)}$ es el vector de características, $y^{(i)}$ es la etiqueta real y $\sigma(z)$ es la función sigmoide.

Para minimizar $J(w, b)$ se calculan las derivadas parciales respecto a cada parámetro, lo que permite estimar la pendiente de la función de coste en un punto dado. Estas derivadas se expresan como

\frac{\partial J}{\partial w} = dw = \frac{1}{M} \sum_{i=1}^{M} (\hat{y}^{(i)} - y^{(i)}) x^{(i)},

\frac{\partial J}{\partial b} = db = \frac{1}{M} \sum_{i=1}^{M} (\hat{y}^{(i)} - y^{(i)}),

y representan la dirección en la que deben modificarse los parámetros $w$ y $b$ para reducir el error.

El procedimiento iterativo comienza con la inicialización de los parámetros con valores pequeños, ya sea ceros o aleatorios. A continuación, se realiza la propagación hacia adelante para calcular las predicciones $\hat{y}$ a partir de los datos de entrada $X$ y se evalúa la función de pérdida $\mathcal{L}(\hat{y}, y)$ y la función de coste $J(w, b)$ sobre el conjunto de entrenamiento. Posteriormente se aplica la propagación hacia atrás para calcular las derivadas parciales $dw$ y $db$ , que se utilizan para actualizar los parámetros mediante la regla

w := w - \alpha \cdot dw,

\quad b := b - \alpha \cdot db,

donde $\alpha$ es la tasa de aprendizaje que regula el tamaño del paso en cada iteración.

Cada actualización mueve los parámetros en la dirección opuesta al gradiente, asegurando la reducción del valor de la función de coste. Este proceso se repite de manera iterativa hasta que el modelo converge a un mínimo adecuado de $J(w, b)$ , momento en el cual las actualizaciones se vuelven insignificantes y las predicciones alcanzan la precisión deseada.

En la práctica, estos cálculos se implementan mediante vectorización, utilizando operaciones matriciales que permiten procesar todos los ejemplos simultáneamente. La vectorización simplifica la implementación, reduce el tiempo de entrenamiento y aprovecha de manera eficiente la capacidad de cálculo de las GPUs, lo que resulta crucial en aplicaciones de Deep Learning con grandes volúmenes de datos.

2.4. Implementación de la regresión logística

A continuación se muestra una implementación básica de regresión logística empleando Python y la librería NumPy. Este ejemplo abarca desde la inicialización de los parámetros hasta su actualización mediante descenso del gradiente y la generación de predicciones finales, ofreciendo una referencia práctica para comprender el funcionamiento y la implementación de la regresión logística en problemas de clasificación binaria.

import numpy as np
import matplotlib.pyplot as plt

# 1. Dataset de ejemplo
np.random.seed(1)
m = 200  # número de ejemplos
n = 2    # número de características

# Clase 0
X0 = np.random.randn(m//2, n) + np.array([-2, -2])
Y0 = np.zeros((m//2, 1))

# Clase 1
X1 = np.random.randn(m//2, n) + np.array([2, 2])
Y1 = np.ones((m//2, 1))

# Concatenar y transponer
X = np.vstack((X0, X1)).T
Y = np.vstack((Y0, Y1)).T

# 2. Funciones auxiliares
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def initialize_params(n):
    w = np.zeros((n, 1))
    b = 0
    return w, b

def forward_propagation(w, b, X, Y):
    m = X.shape[1]
    Z = np.dot(w.T, X) + b
    A = sigmoid(Z)
    cost = -(1/m) * np.sum(Y*np.log(A) + (1-Y)*np.log(1-A))
    return A, cost

def backward_propagation(A, X, Y):
    m = X.shape[1]
    dw = (1/m) * np.dot(X, (A - Y).T)
    db = (1/m) * np.sum(A - Y)
    return dw, db

def update_params(w, b, dw, db, learning_rate):
    w -= learning_rate * dw
    b -= learning_rate * db
    return w, b

# 3. Entrenamiento
def logistic_regression(X, Y, num_iterations=1000, learning_rate=0.1, print_cost=False):
    n = X.shape[0]
    w, b = initialize_params(n)
    costs = []

    for i in range(num_iterations):
        A, cost = forward_propagation(w, b, X, Y)
        dw, db = backward_propagation(A, X, Y)
        w, b = update_params(w, b, dw, db, learning_rate)

        if i % 100 == 0:
            costs.append(cost)
            if print_cost:
                print(f"Iteración {i}: coste = {cost:.4f}")

    return w, b, costs

# 4. Predicción
def predict(w, b, X):
    A = sigmoid(np.dot(w.T, X) + b)
    return (A > 0.5).astype(int)

# 5. Entrenar y evaluar
w, b, costs = logistic_regression(X, Y, num_iterations=1000, learning_rate=0.1, print_cost=True)
Y_pred = predict(w, b, X)
accuracy = 100 - np.mean(np.abs(Y_pred - Y)) * 100
print(f"\nExactitud del modelo: {accuracy:.2f}%")

# 6. Visualización
plt.plot(costs)
plt.xlabel("Iteraciones (x100)")
plt.ylabel("Coste")
plt.title("Reducción del coste durante el entrenamiento")
plt.show()

3. Redes neuronales y funciones de activación

3.1. Generalización y sobreajuste

Un modelo que presenta un coste bajo en el conjunto de entrenamiento no necesariamente constituye un buen modelo. Esta situación puede indicar la presencia de sobreajuste (overfitting), un fenómeno que ocurre cuando la precisión obtenida en los datos de entrenamiento es significativamente mayor que en los conjuntos de validación o prueba. En estos casos, el modelo no aprende patrones generales de los datos, sino que memoriza ejemplos específicos, lo que reduce su capacidad de generalizar a datos nuevos y limita su utilidad práctica.

El sobreajuste suele manifestarse cuando existen pocas muestras disponibles para entrenar, cuando se emplean arquitecturas excesivamente complejas, o cuando los datos presentan problemas de representación, tales como etiquetado incorrecto, predominancia de ciertas clases sobre otras (desequilibrio de clases) o sesgos en el conjunto de datos. Además, las variaciones en las distribuciones de los datos entre el entrenamiento y el uso en producción pueden afectar la capacidad del modelo para generalizar correctamente.

3.2. De neuronas a redes neuronales

Una neurona artificial se puede representar de manera similar a una regresión logística: recibe entradas, las combina linealmente mediante pesos y sesgo, y aplica una función de activación para producir una salida. No obstante, la regresión lineal presenta limitaciones al modelar relaciones complejas en los datos. Para superar estas limitaciones, es necesario aumentar la capacidad de representación de las neuronas.

Una red neuronal se construye al apilar múltiples neuronas organizadas en capas, interconectadas entre sí, de manera que la información procesada por una neurona puede transmitirse a otras neuronas de la misma capa o de capas posteriores. Este mecanismo permite que cada neurona transfiera la representación que ha generado de los datos de entrada a las neuronas siguientes. Las arquitecturas de redes neuronales incluyen diferentes tipos de capas:

La capa de entrada recibe las características iniciales de los datos.
La capa de salida produce la predicción final.
Las capas ocultas, situadas entre la capa de entrada y la de salida, transforman progresivamente la información. Se denominan "ocultas" porque sus valores no se observan directamente, sino que únicamente se percibe su efecto en la salida final.

El cálculo de la salida de una red neuronal consiste en aplicar repetidamente la operación de combinación lineal seguida de activación. La complejidad del aprendizaje profundo aumenta con el número de capas y conexiones, incrementando la capacidad de representación del modelo, pero también dificultando su interpretación.

3.3. Funciones de activación

Las funciones de activación introducen no linealidad en la red neuronal, permitiendo que el modelo aprenda relaciones complejas entre los datos. Sin funciones de activación, una red neuronal se reduce a una combinación lineal de las entradas, comportándose de manera similar a métodos clásicos no basados en redes neuronales. La elección de la función de activación es fundamental y depende del tipo de capa y del problema a resolver.

En las capas ocultas, se emplean funciones de activación como:

ReLU (Rectified Linear Unit): Es ampliamente utilizada en redes profundas, ya que acelera el entrenamiento y evita problemas de gradientes muy pequeños. No obstante, puede provocar neuronas muertas, que siempre devuelven cero. Para mitigar este efecto se utilizan variantes como Leaky ReLU, que mantiene un pequeño gradiente para valores negativos. Se representa como
$f(x) = \max(0, x).$
Sigmoide: Transforma los valores en el rango $[0,1]$ . Se utiliza en redes recurrentes, aunque presenta el problema de gradientes que desaparecen en los extremos. Se representa como
$\sigma(x) = \frac{1}{1 + e^{-x}}$
Tangente hiperbólica (tanh): Normaliza las salidas en el rango $[-1, 1]$ . Suele preferirse frente a la sigmoide en capas ocultas porque sus activaciones tienen media cercana a cero, lo que facilita el entrenamiento. Tanto la sigmoide como la tangente hiperbólica tienden a saturarse en valores extremos, provocando gradientes muy pequeños que ralentizan el proceso de aprendizaje.
$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

En las capas de salida, la función de activación se selecciona según el rango de valores esperado en la salida:

Clasificación binaria: sigmoide.
Clasificación multiclase (mutuamente excluyentes): softmax, que generaliza la sigmoide para más de dos clases.
Clasificación multietiqueta: sigmoide, ya que una muestra puede pertenecer simultáneamente a varias clases.
Regresión: activación lineal, permitiendo que la salida adopte cualquier valor real.

3.4. Implementación de una red neuronal

El siguiente ejemplo implementa una red neuronal de dos capas para un conjunto de datos sintético. Este código ilustra de manera práctica cómo construir, entrenar y evaluar una red neuronal simple utilizando ReLU en la capa oculta y sigmoide en la capa de salida para un problema de clasificación binaria. La red aprende a identificar la relación entre las características de entrada y la clase de salida, mostrando cómo la combinación de forward y backward propagation permite ajustar los parámetros mediante optimización basada en gradientes.

import numpy as np
import matplotlib.pyplot as plt

# --
# 1. Crear dataset sintético
# --
np.random.seed(0)
m = 200  # número de ejemplos
X = np.random.randn(2, m)  # 2 características
Y = (X[0, :] * X[1, :] > 0).astype(int).reshape(1, m)
# Clase = 1 si x1 y x2 tienen el mismo signo, si no 0

# --
# 2. Funciones auxiliares
# --
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def relu(z):
    return np.maximum(0, z)

def relu_derivative(z):
    return (z > 0).astype(float)

def compute_loss(Y, A):
    m = Y.shape[1]
    return -(1/m) * np.sum(Y*np.log(A+1e-8) + (1-Y)*np.log(1-A+1e-8))

# --
# 3. Inicializar parámetros
# --
def initialize_parameters(n_x, n_h, n_y):
    np.random.seed(1)
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    return {"W1": W1, "b1": b1, "W2": W2, "b2": b2}

# --
# 4. Forward propagation
# --
def forward_propagation(X, params):
    W1, b1, W2, b2 = params["W1"], params["b1"], params["W2"], params["b2"]
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)
    cache = {"Z1": Z1, "A1": A1, "Z2": Z2, "A2": A2}
    return A2, cache

# --
# 5. Backpropagation
# --
def backward_propagation(X, Y, params, cache):
    m = X.shape[1]
    W2 = params["W2"]
    A1, A2, Z1 = cache["A1"], cache["A2"], cache["Z1"]

    dZ2 = A2 - Y
    dW2 = (1/m) * np.dot(dZ2, A1.T)
    db2 = (1/m) * np.sum(dZ2, axis=1, keepdims=True)

    dA1 = np.dot(W2.T, dZ2)
    dZ1 = dA1 * relu_derivative(Z1)
    dW1 = (1/m) * np.dot(dZ1, X.T)
    db1 = (1/m) * np.sum(dZ1, axis=1, keepdims=True)

    return {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}

# --
# 6. Actualizar parámetros
# --
def update_parameters(params, grads, lr):
    params["W1"] -= lr * grads["dW1"]
    params["b1"] -= lr * grads["db1"]
    params["W2"] -= lr * grads["dW2"]
    params["b2"] -= lr * grads["db2"]
    return params

# --
# 7. Entrenamiento
# --
def model(X, Y, n_h=3, num_iterations=10000, lr=0.1, print_loss=True):
    n_x, n_y = X.shape[0], Y.shape[0]
    params = initialize_parameters(n_x, n_h, n_y)

    for i in range(num_iterations):
        A2, cache = forward_propagation(X, params)
        loss = compute_loss(Y, A2)
        grads = backward_propagation(X, Y, params, cache)
        params = update_parameters(params, grads, lr)

        if print_loss and i % 1000 == 0:
            print(f"Iteración {i}, pérdida: {loss:.4f}")

    return params

# --
# 8. Predicciones
# --
def predict(X, params):
    A2, _ = forward_propagation(X, params)
    return (A2 > 0.5).astype(int)

# --
# 9. Ejecutar el modelo
# --
params = model(X, Y, n_h=3, num_iterations=10000, lr=0.1)
Y_pred = predict(X, params)
acc = np.mean(Y_pred == Y) * 100
print(f"Precisión final: {acc:.2f}%")

4. Introducción a las redes neuronales profundas

Las redes neuronales profundas constituyen una extensión de las redes neuronales artificiales tradicionales y parten de los mismos fundamentos ya estudiados. Su principal diferencia radica en la presencia de múltiples capas ocultas, dispuestas de manera secuencial como una pila, lo que permite construir representaciones jerárquicas de la información. Dichas representaciones reflejan un nivel progresivo de conocimiento que se amplía tanto en profundidad como en amplitud. La amplitud depende del número de parámetros aprendibles de cada capa, como ocurre con la cantidad de neuronas en una capa densa o con el número de canales y filtros en las capas convolucionales, que se analizarán en capítulos posteriores.

En este contexto, las primeras capas de la red, situadas cerca de la entrada, poseen una capacidad limitada para reconocer patrones complejos y suelen detectar únicamente características elementales. Por ejemplo, en arquitecturas diseñadas para procesar imágenes, las capas iniciales tienden a identificar líneas horizontales, verticales o diagonales. Conforme se avanza hacia capas más profundas, las representaciones se vuelven progresivamente más sofisticadas, ya que se construyen combinando las características detectadas en etapas anteriores. De este modo, en niveles intermedios es posible identificar formas más estructuradas, mientras que en las capas finales se logran representaciones de alto nivel que corresponden a objetos completos o conceptos abstractos.

Este proceso resulta coherente porque la red aplica de manera sucesiva operaciones no lineales que integran y transforman la información proveniente de distintas características. Cada capa contribuye con una representación parcial que, al combinarse con las anteriores, incrementa la complejidad y la capacidad de entendimiento del modelo. En consecuencia, las redes neuronales profundas destacan por su habilidad para aprender patrones complejos y abstractos a partir de grandes volúmenes de datos diversos, lo que las convierte en una herramienta esencial en el campo del aprendizaje automático y la inteligencia artificial.

La principal motivación para utilizar redes profundas radica precisamente en esta capacidad de aprender representaciones jerárquicas. Las primeras capas tienden a detectar características elementales, como bordes en imágenes o frecuencias simples en señales de audio. Las capas intermedias combinan dichas características para identificar estructuras más complejas, como formas, texturas o partes específicas de un objeto. Finalmente, las capas más profundas integran la información previa y logran representar entidades completas, como rostros, palabras o categorías semánticas. Cuanto mayor es la profundidad de la red, mayor es la capacidad para modelar patrones de alta complejidad.

4.1. Parámetros e hiperparámetros

En el entrenamiento de redes neuronales profundas resulta esencial distinguir entre parámetros e hiperparámetros. Los parámetros incluyen los pesos y sesgos de la red, los cuales se aprenden automáticamente mediante algoritmos de optimización. Los hiperparámetros, en cambio, se definen antes del entrenamiento y controlan aspectos estructurales y dinámicos del modelo. Entre ellos destacan la tasa de aprendizaje, el número de iteraciones o épocas, la cantidad de capas ocultas, el número de neuronas por capa y la elección de funciones de activación. La búsqueda de hiperparámetros constituye un proceso iterativo en el que se combinan prueba y error con estrategias más sistemáticas, con el fin de encontrar la configuración que produzca el mejor desempeño.

4.2. Propagación hacia delante

La propagación hacia delante consiste en transformar las entradas de la red en salidas mediante operaciones sucesivas en cada capa. En una capa $L$ , la salida se obtiene al multiplicar la matriz de pesos de esa capa por las activaciones de la capa anterior $(L-1)$ , sumando un sesgo y aplicando posteriormente una función de activación que introduce no linealidad en el modelo. Esta no linealidad es fundamental, ya que permite a la red aproximar funciones complejas que no podrían ser representadas únicamente mediante combinaciones lineales.

En cuanto a las dimensiones, la matriz de pesos de la capa $L$ tiene forma $(N_L, N_{L-1})$ , donde $N_L$ representa el número de neuronas de la capa actual y $N_{L-1}$ el número de neuronas de la capa anterior. El vector de sesgos presenta dimensiones $(N_L, 1)$ . Durante la propagación hacia atrás, utilizada en el entrenamiento, las derivadas de los pesos y los sesgos mantienen estas mismas dimensiones, lo que asegura la consistencia de los cálculos.

En esta fase ningún parámetro se actualiza, pues únicamente se realizan combinaciones de las entradas con los parámetros existentes de la red. El resultado de cada capa se encadena con la siguiente hasta obtener la salida final. Una vez obtenida esta salida, se calcula la función de pérdida, cuya finalidad es cuantificar el error y servir como guía para ajustar los parámetros aprendibles de la red con el objetivo de alcanzar un mínimo de dicha función.

En aprendizaje supervisado, la pérdida suele medir la diferencia entre las clases predichas y las clases reales del conjunto de entrenamiento, o bien comparar distribuciones para minimizar la distancia entre ellas. En aprendizaje no supervisado, la función de pérdida puede variar. En tareas de reconstrucción se recurre, por ejemplo, al error cuadrático medio, mientras que en escenarios de representación o agrupamiento se utilizan métricas de distancia. Un caso particular es el aprendizaje contrastivo, ampliamente utilizado en el aprendizaje autosupervisado, que busca acercar representaciones de ejemplos similares y alejar aquellas correspondientes a ejemplos diferentes. La función de coste se define para cada muestra individual, pero cuando se calcula sobre todo el conjunto de entrenamiento y se promedia, se denomina función de pérdida.

4.3. Propagación hacia atrás y optimización

En las redes neuronales profundas, no solo se requiere calcular la propagación hacia delante, sino también actualizar de manera sistemática los parámetros que definen el modelo. Una vez obtenida la salida y evaluada mediante una función de pérdida, se aplica la propagación hacia atrás (backpropagation) con el objetivo de reducir progresivamente el error. Este procedimiento constituye el núcleo del aprendizaje en redes profundas y se apoya en algoritmos de optimización que orientan el ajuste de pesos y sesgos.

El proceso inicia con el cálculo de los gradientes, que representan las derivadas parciales de la función de pérdida con respecto a cada parámetro del modelo. Los gradientes indican la dirección de mayor incremento de la pérdida, por lo que desplazarse en la dirección opuesta permite reducirla. El objetivo consiste en alcanzar un mínimo de la función de pérdida, que en la práctica puede ser local, pero resulta suficiente si garantiza un desempeño adecuado. El método más básico de optimización actualiza los parámetros según la regla

\theta_{t+1} = \theta_t - \eta \, \nabla_\theta \mathcal{L}(\theta_t),

donde $\theta$ representa un peso o sesgo, $\eta$ es la tasa de aprendizaje y $\nabla_\theta \mathcal{L}(\theta_t)$ corresponde al gradiente de la función de pérdida en el instante $t$ .

La magnitud del ajuste de los parámetros está gobernada por la tasa de aprendizaje ( $\eta$ ). Una tasa demasiado alta puede provocar oscilaciones e incluso divergencia, mientras que una tasa demasiado baja ralentiza la convergencia. Una estrategia habitual consiste en iniciar con valores relativamente grandes para acelerar las primeras etapas del entrenamiento y reducir progresivamente la magnitud de los pasos conforme se aproxima al mínimo, evitando así desestabilizar el proceso.

Para mejorar la eficiencia, en lugar de calcular los gradientes utilizando el conjunto completo de datos, se emplea el descenso de gradiente estocástico (SGD), que utiliza pequeños subconjuntos (mini-batches). Esta aproximación introduce aleatoriedad, disminuye el coste computacional y ayuda a escapar de regiones problemáticas, como los puntos de silla, donde los gradientes se anulan sin representar un mínimo real.

El descenso de gradiente básico puede resultar ineficiente en ciertos escenarios, por lo que se han desarrollado variantes que mejoran su rendimiento. Una de ellas es el algoritmo Momentum, que introduce un efecto de inercia acumulando información de gradientes previos para suavizar las actualizaciones. Se define mediante las ecuaciones

v_t = \beta v_{t-1} + (1-\beta) \, \nabla_\theta \mathcal{L}(\theta_t),

\theta_{t+1} = \theta_t - \eta \, v_t,

donde $v_t$ representa la “velocidad” acumulada y $\beta \in [0,1)$ es el coeficiente de decaimiento, generalmente fijado en 0.9. Este mecanismo reduce las oscilaciones en direcciones de alta curvatura y acelera la convergencia en valles estrechos.

Otro método es RMSprop, que adapta la tasa de aprendizaje a cada parámetro mediante el escalado de los gradientes por una media móvil de sus valores al cuadrado

s_t = \rho s_{t-1} + (1-\rho) \left(\nabla_\theta \mathcal{L}(\theta_t)\right)^2,

\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{s_t + \epsilon}} \, \nabla_\theta \mathcal{L}(\theta_t),

donde $\rho \approx 0.9$ y $\epsilon \approx 10^{-8}$ para evitar divisiones por cero. Este ajuste permite que los parámetros con gradientes grandes reciban pasos más pequeños, mientras que aquellos con gradientes pequeños se actualizan más rápidamente, mejorando la estabilidad del entrenamiento.

El optimizador Adam combina las ventajas de Momentum y RMSprop, acumulando tanto la media de los gradientes como la media de sus cuadrados. Su formulación se realiza en cuatro etapas.

Media de gradientes (primer momento):

m_t = \beta_1 m_{t-1} + (1-\beta_1) \, \nabla_\theta \mathcal{L}(\theta_t).

Media de cuadrados de gradientes (segundo momento):

v_t = \beta_2 v_{t-1} + (1-\beta_2) \, \left(\nabla_\theta \mathcal{L}(\theta_t)\right)^2.

Corrección del sesgo inicial:

\hat{m}_t = \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t}.

Actualización final de los parámetros:

\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \, \hat{m}_t.

Los valores recomendados son $\beta_1 = 0.9$ , $\beta_2 = 0.999$ y $\epsilon = 10^{-8}$ . Este optimizador se utiliza ampliamente debido a su rapidez, estabilidad y robustez frente a configuraciones no óptimas de hiperparámetros.

4.3.1. Implementación de optimizadores

A modo de ilustración, se presenta una implementación de los principales optimizadores aplicada a la función de prueba $f(\theta) = \theta^2$ , cuyo mínimo global se encuentra en $\theta=0$ . En este ejemplo, todos los optimizadores parten de un valor inicial $\theta=5$ y buscan reducir la función de pérdida. Aunque cada algoritmo sigue trayectorias distintas, todos tienden hacia el mínimo global en $\theta=0$ .

import numpy as np

# Función de pérdida y gradiente
loss = lambda theta: theta**2
grad = lambda theta: 2*theta

# Valor inicial
theta_init = 5.0

# Descenso de gradiente estocástico (SGD)
def sgd(theta, grad, eta=0.1, steps=20):
    for t in range(steps):
        theta -= eta * grad(theta)
    return theta

# Momentum
def momentum(theta, grad, eta=0.1, beta=0.9, steps=20):
    v = 0
    for t in range(steps):
        v = beta * v + (1 - beta) * grad(theta)
        theta -= eta * v
    return theta

# RMSprop
def rmsprop(theta, grad, eta=0.1, rho=0.9, eps=1e-8, steps=20):
    s = 0
    for t in range(steps):
        g = grad(theta)
        s = rho * s + (1 - rho) * g**2
        theta -= eta / (np.sqrt(s) + eps) * g
    return theta

# Adam
def adam(theta, grad, eta=0.1, beta1=0.9, beta2=0.999, eps=1e-8, steps=20):
    m, v = 0, 0
    for t in range(1, steps+1):
        g = grad(theta)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * g**2
        m_hat = m / (1 - beta1**t)
        v_hat = v / (1 - beta2**t)
        theta -= eta / (np.sqrt(v_hat) + eps) * m_hat
    return theta

print("SGD:", sgd(theta_init, grad))
print("Momentum:", momentum(theta_init, grad))
print("RMSprop:", rmsprop(theta_init, grad))
print("Adam:", adam(theta_init, grad))

4.4. División del conjuntos de datos

En el entrenamiento de modelos de aprendizaje automático y, en particular, de redes neuronales profundas, la gestión adecuada de los datos constituye un paso fundamental para garantizar un proceso de optimización eficiente y una evaluación rigurosa del rendimiento.

Como se mencionó anteriormente, uno de los enfoques empleados para agilizar el descenso del gradiente es el descenso de gradiente estocástico. Esta técnica permite aplicar el algoritmo de optimización no sobre la totalidad del conjunto de entrenamiento, sino sobre subconjuntos de datos. Al evaluar el gradiente en un lote reducido, se obtiene información temprana sobre el progreso de la optimización sin necesidad de procesar todas las muestras, lo que facilita un aprendizaje más rápido y actualizaciones de los parámetros del modelo con mayor frecuencia.

El uso de lotes resulta especialmente ventajoso en entornos con GPU, ya que estas permiten almacenar los datos en memoria gráfica y ejecutar cálculos de manera altamente paralelizada. El tamaño de los lotes depende principalmente de la capacidad de memoria disponible, siendo comunes valores como 32, 64, 128 o superiores. Aunque frecuentemente se prefieren potencias de dos, esta elección no conlleva necesariamente una mejora en la eficiencia, por lo que pueden emplearse otros valores sin detrimento del rendimiento. En general, se tiende a utilizar lotes tan grandes como lo permita la memoria, aunque el tamaño seleccionado puede afectar las métricas de evaluación del modelo. Por ejemplo, en arquitecturas basadas en autoencoders, se observa un mejor desempeño con lotes pequeños, ya que esto limita la tendencia de la red a memorizar patrones específicos. En contraste, en tareas supervisadas de clasificación de imágenes o en metodologías contrastivas, los lotes más grandes suelen ser beneficiosos, ya que permiten calcular un mayor número de métricas de distancia entre pares de muestras y construir matrices de similitud más robustas, mejorando así la calidad de las representaciones aprendidas.

En contextos de aprendizaje auto-supervisado, el modo en que se agrupan las muestras en lotes afecta directamente tanto a las funciones de coste como al proceso de optimización. Esto se debe a que muchas de estas funciones se basan en medidas de distancia entre elementos de un mismo lote. La inclusión de un mayor número de muestras similares o variadas dentro de un lote puede modificar sustancialmente las estadísticas empleadas en el aprendizaje, especialmente cuando se aplican técnicas de normalización por lotes o por capas.

Incluso en modelos de lenguaje de gran escala se ha observado que la forma de dividir los datos en lotes repercute en la salida final del modelo. A pesar de que las capas de estos modelos son deterministas y que parámetros como la temperatura de muestreo podrían sugerir resultados estables, en la práctica se generan salidas distintas para una misma entrada. Parte de esta variabilidad se explica no solo por errores numéricos o de redondeo, sino también por la manera en que se conforman los mini-lotes y las distribuciones de las muestras que los componen.

De manera clásica, durante el desarrollo de modelos de aprendizaje automático los conjuntos de datos se dividen en tres subconjuntos principales:

Conjunto de entrenamiento: Se emplea para ajustar los parámetros internos del modelo mediante el proceso de optimización. Puede contener o no etiquetas.
Conjunto de validación: Formado por ejemplos no utilizados en el entrenamiento directo. Su función es evaluar la capacidad de generalización del modelo y guiar la selección de hiperparámetros, reduciendo el riesgo de sobreajuste.
Conjunto de prueba: Reservado para la evaluación final y objetiva del modelo una vez completado el entrenamiento y optimizados los hiperparámetros.

La proporción destinada a cada subconjunto depende de la cantidad de datos disponibles. Con bases de datos pequeñas, se suele aplicar una partición del 70 % para entrenamiento y 30 % para prueba. En bases de datos más extensas, resulta común asignar un 60 % al entrenamiento, 20 % a la validación y 20 % a la prueba. Es esencial que los subconjuntos de validación y prueba sigan la misma distribución que los datos de entrenamiento, ya que una discrepancia significativa puede generar degradaciones en las métricas de evaluación.

En entornos de producción este problema es frecuente, dado que las distribuciones de los datos suelen variar con el tiempo. Por ejemplo, en sistemas de telecomunicaciones, los patrones de uso de los usuarios pueden cambiar drásticamente entre diferentes épocas del año, lo que ocasiona desviaciones entre los datos de entrenamiento y los datos reales en producción. Para detectar y cuantificar estas desviaciones se utilizan métricas como la divergencia de Kullback-Leibler, la divergencia de Jensen-Shannon u otras medidas de distancia entre distribuciones. Asimismo, técnicas como el análisis de entropía, los autoencoders o el Análisis de Componentes Principales (PCA) permiten medir errores de reconstrucción y establecer umbrales (por ejemplo, basados en percentiles) para identificar muestras fuera de distribución.

La detección de datos fuera de distribución constituye una línea de investigación activa dentro del aprendizaje profundo, con aplicaciones en el aprendizaje activo, el meta learning y la mitigación del olvido catastrófico. Estas metodologías buscan adaptar los modelos a nuevos datos de producción no observados previamente, ampliando su conocimiento sin necesidad de reentrenarlos por completo. En ciertos casos, se investiga la posibilidad de incorporar nuevos datos sin requerir acceso a los datos originales, lo que resulta especialmente relevante en contextos donde estos ya no están disponibles. Un ejemplo claro se encuentra en las telecomunicaciones, donde la transición de tecnologías como 4G a 5G exige reutilizar modelos entrenados con datos de la generación anterior, pese a que estos no puedan recuperarse, lo que demanda estrategias capaces de transferir conocimiento sin perder la información previa.

4.5. Sesgo y varianza

El análisis de sesgo y varianza constituye una herramienta fundamental para comprender las fuentes de error en los modelos de aprendizaje automático. Ambos conceptos permiten diagnosticar si un modelo está fallando por su incapacidad para representar correctamente el problema subyacente o por su exceso de adaptación a los datos disponibles.

El sesgo se define como la diferencia sistemática entre las predicciones del modelo y los valores reales. Un sesgo alto indica la presencia de subajuste, lo que significa que el modelo no logra capturar de manera adecuada la complejidad de la relación existente en los datos. En este caso, las predicciones tienden a ser demasiado simples o alejadas de la realidad, aun cuando se disponga de una gran cantidad de datos de entrenamiento.

Por otro lado, la varianza mide la sensibilidad del modelo frente a pequeñas variaciones en los datos de entrenamiento. Una varianza alta refleja la existencia de sobreajuste, fenómeno en el que el modelo se ajusta excesivamente a los ejemplos utilizados en el entrenamiento, incorporando incluso el ruido presente en ellos, lo que impide una correcta generalización hacia datos nuevos.

La reducción del sesgo suele requerir un aumento en la capacidad de representación del modelo. Esto puede lograrse mediante arquitecturas más profundas o complejas, el incremento del número de parámetros, un mayor tiempo de entrenamiento o la adopción de algoritmos alternativos que permitan capturar de manera más fiel las dependencias de los datos. En contraste, para disminuir la varianza se recurre a estrategias orientadas a mejorar la capacidad de generalización, tales como el incremento de la cantidad y diversidad de datos de entrenamiento, la aplicación de técnicas de regularización (como dropout, penalizaciones de norma $L_1$ o $L_2$ ), así como ajustes en la arquitectura y en los hiperparámetros del modelo.

En la práctica, el análisis de sesgo y varianza se complementa con la noción de techo de referencia humano, empleado para evaluar modelos cuyo desempeño se compara con el nivel de expertos humanos en una tarea específica. En este marco, se introduce el concepto de sesgo evitable, entendido como la diferencia entre el error mínimo alcanzable por un ser humano y el error observado en el modelo. A su vez, la varianza se cuantifica como la diferencia entre el error en el conjunto de entrenamiento y el error en el conjunto de validación.

4.6. Métodos de regularización y normalización

La regularización y la normalización son técnicas fundamentales para mejorar la capacidad de generalización de los modelos de aprendizaje profundo y reducir el riesgo de sobreajuste. Ambas estrategias buscan limitar la dependencia excesiva del modelo respecto a los datos de entrenamiento, promoviendo representaciones más robustas y estables que permitan un rendimiento consistente en datos no vistos.

Entre las técnicas de regularización más utilizadas destacan:

Regularización L2 (ridge): Añade una penalización proporcional al cuadrado de los pesos del modelo. Esta restricción evita que los parámetros adquieran valores demasiado grandes, estabiliza la optimización y favorece soluciones más suaves y generalizables.
Regularización L1 (lasso): Penaliza la magnitud absoluta de los pesos, induciendo que muchos de ellos se reduzcan a cero. Esto simplifica el modelo al conservar únicamente las variables más relevantes, actuando además como un método de selección de características.
Dropout: Desactiva aleatoriamente un subconjunto de neuronas durante el entrenamiento, impidiendo que las unidades desarrollen dependencias excesivas entre sí. Esto obliga a la red a generar representaciones redundantes y más robustas. Durante la inferencia, todas las neuronas se utilizan, con los pesos ajustados de forma apropiada.
Aumentación de datos (data augmentation): Crea ejemplos adicionales a partir de transformaciones aplicadas a los datos originales, como rotaciones, traslaciones, cambios de escala o variaciones de iluminación. Esta técnica incrementa la diversidad del conjunto de entrenamiento y hace que el modelo sea menos sensible a variaciones irrelevantes.
Detención temprana (early stopping): Supervisa el rendimiento del modelo sobre el conjunto de validación y detiene el entrenamiento cuando el error deja de mejorar, evitando que la red se ajuste demasiado a las particularidades del conjunto de entrenamiento.
Normalización de entradas: Escala y centra las características de los datos para garantizar magnitudes comparables, acelerando la convergencia, mejorando la estabilidad numérica y evitando que ciertos parámetros dominen el aprendizaje.

En complemento a la regularización, las técnicas de normalización de activaciones resultan esenciales para estabilizar el entrenamiento y acelerar la convergencia. Durante la optimización, las activaciones pueden variar significativamente entre capas, lo que genera inestabilidad y dificulta el ajuste de los parámetros. La normalización busca mantener distribuciones equilibradas de las activaciones a lo largo de la red.

Batch Normalization: Normaliza las activaciones de cada capa utilizando la media y la varianza calculadas sobre los ejemplos de un mini-lote. Esto reduce el problema del internal covariate shift, acelera el aprendizaje, permite tasas de aprendizaje más altas y simplifica el ajuste de hiperparámetros. Sin embargo, su efectividad depende del tamaño y la composición de los lotes, siendo menos adecuada en lotes pequeños o en datos con distribuciones muy variables.
Layer Normalization: Normaliza las activaciones a nivel de capa, calculando estadísticas por muestra en lugar de por mini-lote. Es especialmente útil en arquitecturas secuenciales, como los transformadores, y en escenarios de entrenamiento distribuido, ya que no requiere compartir estadísticas entre lotes, facilitando la paralelización y la escalabilidad. A diferencia de Batch Normalization, proporciona mayor estabilidad en situaciones donde la composición de los lotes puede variar significativamente.

4.7. Desvanecimiento y explosión de gradientes

Uno de los principales desafíos en el entrenamiento de redes neuronales profundas es el fenómeno conocido como desvanecimiento o explosión de gradientes. Ambos problemas se presentan durante el proceso de backpropagation, cuando los gradientes de los parámetros (es decir, las derivadas parciales de la función de pérdida respecto a los pesos) tienden a disminuir hasta valores cercanos a cero o, por el contrario, a crecer de manera exponencial. Esta inestabilidad dificulta o incluso imposibilita el aprendizaje, ya que los parámetros no se actualizan de manera adecuada. En la práctica, este comportamiento puede provocar que la función de pérdida devenga en valores NaN (Not a Number), interrumpiendo el proceso de optimización.

El desvanecimiento de gradientes ocurre cuando los valores derivados se reducen progresivamente en cada capa durante el proceso de backpropagation. Esto provoca que las capas más cercanas a la entrada reciban señales de error muy débiles, limitando la capacidad del modelo para aprender representaciones jerárquicas profundas. Por otro lado, la explosión de gradientes se manifiesta cuando los valores derivados aumentan exponencialmente a medida que se propagan hacia atrás, generando actualizaciones de parámetros excesivamente grandes y conduciendo a un entrenamiento inestable o divergente.

Diversos factores contribuyen a la aparición de estos problemas, destacando especialmente el tipo de inicialización de pesos, la elección de las funciones de activación y la profundidad de la red. En arquitecturas recurrentes tradicionales, como las redes neuronales recurrentes simples (RNN) o incluso las LSTM, el cálculo iterativo de múltiples derivadas sobre secuencias largas amplifica la tendencia a sufrir desvanecimiento o explosión. Esto se debe, en gran medida, al uso de funciones de activación como la tangente hiperbólica o la sigmoide, cuyos rangos limitados y simetría alrededor de valores fijos provocan que los gradientes se saturen en los extremos, reduciendo la señal útil para el aprendizaje.

Para mitigar estos fenómenos se emplean diversas estrategias:

Inicialización adecuada de los pesos: Métodos como Xavier o He ajustan la escala inicial de los parámetros según la cantidad de neuronas por capa, evitando que los gradientes crezcan o decrezcan de manera descontrolada desde el inicio del entrenamiento.
Normalización de los datos de entrada: Escalar las características de entrada para que tengan media cero y varianza unitaria contribuye a estabilizar el flujo de gradientes durante la retropropagación.
Funciones de activación más estables: El uso de activaciones como ReLU y sus variantes (Leaky ReLU, ELU, entre otras) reduce la saturación observada en funciones como la sigmoide o la tangente hiperbólica, favoreciendo gradientes más consistentes.
Clipado de gradientes: Consiste en limitar el rango de valores que pueden alcanzar los gradientes durante la retropropagación. Cuando los gradientes exceden un umbral predefinido, se ajustan a dicho límite, evitando actualizaciones excesivas. Es común emplear intervalos como $\[-1, 1]$ , aunque también existen variantes dinámicas que adaptan este rango según el estado del entrenamiento.
Diseño arquitectónico específico: La introducción de mecanismos de memoria y compuertas en redes como LSTM o GRU permite manejar dependencias de largo plazo, reduciendo los problemas de desvanecimiento de gradientes. Más recientemente, los Transformers han reemplazado en gran medida a las RNN en el procesamiento de secuencias reduciendo estas limitaciones.

4.8. Estrategia en el proceso de optimización

El diseño de una estrategia adecuada en el desarrollo de modelos de aprendizaje automático resulta crucial para alcanzar un rendimiento óptimo y garantizar la utilidad práctica de los sistemas. No todas las mejoras introducidas durante el proceso de construcción del modelo tienen el mismo impacto en su desempeño. En muchos casos, incrementar la cantidad y diversidad de datos disponibles o modificar de manera sustancial la arquitectura de la red genera beneficios mucho mayores que ajustes menores sobre los hiperparámetros. Por este motivo, se requiere establecer métricas claras y bien definidas que orienten las decisiones y permitan evaluar de manera objetiva cada iteración del proceso.

Las métricas de evaluación dependen directamente del tipo de aprendizaje empleado (supervisado, no supervisado o por refuerzo), aunque comparten el objetivo común de cuantificar la calidad de las predicciones. En aprendizaje supervisado de clasificación, destacan medidas como la precisión, que expresa la proporción de verdaderos positivos entre todas las predicciones positivas, el recall o sensibilidad, que calcula la proporción de verdaderos positivos sobre el total de casos positivos reales, y la puntuación F1, definida como la media armónica entre la precisión y el recall, que equilibra ambas perspectivas.

Más allá de las métricas de exactitud, es indispensable considerar indicadores de eficiencia computacional, tales como el tiempo de entrenamiento, la latencia en la inferencia, el consumo de memoria y la escalabilidad del modelo. Estas métricas permiten valorar no solo el grado de acierto, sino también la viabilidad práctica de la solución en contextos de producción. Asimismo, en entornos empresariales resulta común integrar indicadores de impacto económico y de experiencia de usuario, como el retorno de inversión, la satisfacción percibida, la calidad de las respuestas o los tiempos de espera, de manera que el rendimiento técnico se vincule con objetivos estratégicos.

Para implementar una estrategia de aprendizaje coherente y sostenible, se recomienda emplear plataformas especializadas en la gestión de experimentos. Estas herramientas permiten registrar y organizar de forma sistemática todos los artefactos generados durante el desarrollo del modelo, incluidos los parámetros de configuración, el número de capas, las funciones de activación utilizadas, la arquitectura adoptada y las métricas obtenidas en cada ejecución. De este modo, se garantiza la replicabilidad de los experimentos, se facilita la comparación justa entre diferentes configuraciones y se optimiza la toma de decisiones. Entre las plataformas más utilizadas se encuentran MLflow, Weights & Biases (wandb) y soluciones similares, que proporcionan entornos integrados para el seguimiento, análisis y visualización de experimentos de aprendizaje automático.

4.9. Aprendizaje por transferencia y multitarea

Además de las arquitecturas tradicionales, en el campo del aprendizaje profundo se han desarrollado enfoques que no constituyen arquitecturas en sí mismas, sino paradigmas de aprendizaje que buscan aprovechar de manera más eficiente los recursos computacionales y los datos disponibles. Entre los más relevantes se encuentran el aprendizaje por transferencia y el aprendizaje multitarea, ambos orientados a mejorar la capacidad de generalización de los modelos y a reducir el coste de entrenamiento.

El aprendizaje por transferencia consiste en reutilizar el conocimiento adquirido por un modelo previamente entrenado en una tarea determinada para aplicarlo en otra tarea relacionada. Por ejemplo, un modelo entrenado para clasificar imágenes en un dominio amplio (como el conjunto de datos ImageNet) puede transferirse a un modelo más específico, encargado de identificar defectos en piezas industriales o clasificar tipos de cultivos a partir de imágenes satelitales. En este contexto, la similitud entre las tareas es un requisito fundamental. No resulta viable transferir directamente el conocimiento de un modelo entrenado en visión por computadora a uno diseñado para procesar texto, ya que las representaciones internas aprendidas difieren por completo.

El grado de reutilización depende en gran medida de la disponibilidad de datos en la nueva tarea. Cuando los datos son escasos, suele reajustarse únicamente la parte final de la red, por ejemplo, las últimas capas densas de un clasificador. Mientras que el resto de la arquitectura se congela, preservando así las representaciones generales previamente aprendidas. En cambio, cuando se dispone de una cantidad suficiente de datos, es posible aplicar un ajuste fino o fine-tuning, que consiste en reentrenar toda la red para adaptar gradualmente los parámetros a las particularidades del nuevo dominio.

El aprendizaje multitarea, por su parte, persigue que un mismo modelo sea capaz de resolver de manera simultánea múltiples problemas relacionados. La idea central es que al compartir representaciones internas entre diferentes tareas, la red aprende descriptores más generales y robustos que benefician a todas ellas. Un ejemplo paradigmático se encuentra en la conducción autónoma, un único modelo puede segmentar imágenes para identificar peatones, carreteras y vehículos, clasificar señales de tráfico, y, al mismo tiempo, predecir trayectorias de otros automóviles o del propio vehículo. En este escenario, el entrenamiento implica optimizar distintas funciones de coste (una para la segmentación, otra para la clasificación y otra para la predicción de movimientos) que se combinan en un proceso conjunto de descenso del gradiente.

5. Arquitecturas de aprendizaje profundo, redes neuronales convolucionales

5.1. Procesamiento visual humano y su analogía con las redes neuronales convolucinales

El procesamiento visual humano es un proceso jerárquico que transforma la información lumínica captada por los ojos en representaciones visuales complejas y significativas. Este proceso involucra múltiples etapas funcionales que van desde la captación inicial de la luz hasta el análisis de formas y objetos en áreas corticales especializadas.

La luz ingresa al ojo a través de la córnea y atraviesa el cristalino, el cual actúa como una lente convexa que invierte la imagen proyectándola sobre la retina, ubicada en la parte posterior del globo ocular. En la retina, los fotorreceptores (conos y bastones) convierten la energía lumínica en señales eléctricas, iniciando así la codificación neuronal de la información visual.

Estas señales se transmiten por el nervio óptico de cada ojo hasta el quiasma óptico, donde ocurre un cruce parcial de la información visual, los campos visuales izquierdos de ambos ojos se dirigen al hemisferio derecho, mientras que los campos visuales derechos se proyectan al hemisferio izquierdo. Esta organización permite la percepción binocular y contribuye a la percepción de profundidad.

Posteriormente, las señales continúan a través del tracto óptico hasta el núcleo geniculado lateral (LGN) del tálamo, que funciona como estación de relevo y organiza la información entrante. El LGN está compuesto por capas diferenciadas que procesan señales provenientes de distintos tipos de células ganglionares, permitiendo un preprocesamiento especializado que facilita el análisis visual posterior.

Desde el LGN, las señales visuales se transmiten mediante las radiaciones ópticas hacia la corteza visual primaria (V1), localizada en el lóbulo occipital. La V1 se organiza de manera retinotópica, de modo que cada región del campo visual se proyecta a un área cortical específica. En esta región, las neuronas responden a patrones visuales básicos mediante campos receptivos, que representan pequeñas regiones del espacio visual a las que responden selectivamente.

En la corteza visual primaria se distinguen tres tipos principales de células. Células simples, que responden a bordes con orientación específica, células complejas, que detectan bordes o movimientos en rangos más amplios, y células hipercomplejas, que reaccionan ante combinaciones más sofisticadas, como esquinas o terminaciones de líneas. El procesamiento continúa en áreas corticales posteriores (V2, V4, IT), donde se analizan características más complejas, incluyendo texturas, formas tridimensionales, rostros y objetos completos.

Las redes neuronales convolucionales, también conocidas como Convolutional Neural Networks (CNNs), son modelos computacionales diseñados para procesar datos visuales de manera eficiente, inspirados directamente en la arquitectura del sistema visual humano, especialmente en la corteza visual primaria. En este contexto, se establecen correspondencias claras entre las estructuras biológicas y los componentes de una red convolucional:

Sistema Visual Humano	Redes Convolucionales (CNNs)
Retina	Imagen de entrada
Nervio óptico / Quiasma óptico	Preprocesamiento y alineación de la información visual
LGN (núcleo geniculado lateral)	División en canales o filtros por tipo de característica
Corteza visual (V1, V2, V4, IT)	Capas convolucionales jerárquicas
Células simples, complejas, hipercomplejas	Filtros convolucionales de bajo, medio y alto nivel
Campos receptivos	Regiones locales (receptive fields) de los filtros (kernels)
Percepción jerárquica	Aprendizaje progresivo de características visuales

En las CNNs, cada unidad procesa únicamente una región limitada de la imagen, análoga a los campos receptivos de las neuronas en V1. Los filtros convolucionales permiten detectar bordes, texturas, formas y patrones complejos, emulando las funciones de las células visuales especializadas. La estructura jerárquica de las CNNs permite que las primeras capas capturen patrones simples, las intermedias estructuras más complejas y las últimas integren estos elementos para identificar objetos completos. Adicionalmente, técnicas como el max pooling reducen la dimensionalidad de manera selectiva, conservando información relevante, similar al resumen jerárquico que realiza el cerebro al procesar escenas visuales complejas.

5.2. Campo receptivo y jerarquía de procesamiento visual

El campo receptivo se define como la región del campo visual que influye directamente en la actividad de una neurona específica. En las etapas iniciales del procesamiento visual, como en V1, los campos receptivos son pequeños y especializados en detectar patrones simples, como líneas u orientaciones. A medida que se avanza jerárquicamente en la corteza visual, los campos receptivos se expanden y se vuelven más complejos, integrando información de múltiples regiones para formar representaciones más abstractas y globales. Por ejemplo, una neurona en una capa inicial de un sistema visual podría tener un campo receptivo de 3×3 píxeles, mientras que en capas sucesivas la combinación de varios campos receptivos previos permite formar unidades con campos más amplios, como 5×5 o 7×7 píxeles. Esta organización favorece la abstracción progresiva y la especialización en el análisis visual.

5.3. Conceptos fundamentales de la convolución

La visión computacional constituye uno de los campos más dinámicos y transformadores de la inteligencia artificial. A través de ella se han desarrollado aplicaciones que abarcan desde la conducción autónoma hasta el reconocimiento facial, la clasificación automática de imágenes y la segmentación de objetos en entornos complejos. La relevancia de este ámbito es tal que sus fundamentos han trascendido el análisis de imágenes, inspirando avances en disciplinas distintas, como el procesamiento del lenguaje natural o el reconocimiento de voz.

El principio subyacente que permite esta transferencia de conocimiento es la existencia de una estructura espacio-temporal en los datos. En el caso de las imágenes, esta estructura se refleja en la disposición relativa de los píxeles. Si se logra transformar otros tipos de datos en representaciones visuales que conserven dicha organización, es posible aplicar arquitecturas convolucionales de manera eficaz. Un ejemplo de este enfoque se observa en la conversión de series temporales en imágenes mediante técnicas como los Gramian Angular Fields. Este método transforma la serie temporal en coordenadas polares y genera una matriz de ángulos que produce una imagen con información espacio-temporal equivalente a la contenida en la secuencia original. De modo similar, las señales de audio pueden convertirse en espectrogramas de tipo Mel, lo que permite aprovechar las propiedades de las redes convolucionales para tareas de clasificación, identificación o análisis acústico.

El principal desafío al trabajar con imágenes radica en la elevada cantidad de información que contienen. Considérese, por ejemplo, una imagen en color de 64 × 64 píxeles. Dado que cada píxel posee tres componentes de color (rojo, verde y azul), la representación requiere tres matrices de 64 × 64 valores, lo que equivale a 12288 entradas para la red neuronal. Introducir directamente esta cantidad de datos en una arquitectura tradicional obligaría a disponer de capas iniciales con decenas de miles de neuronas, lo que genera un coste computacional muy alto y un elevado riesgo de sobreajuste a medida que la resolución de las imágenes aumenta.

La solución a este problema se encuentra en la operación de convolución. Este procedimiento aplica filtros, también denominados kernels, que recorren la imagen en busca de patrones característicos como bordes, esquinas o texturas. El resultado de cada aplicación es un mapa de características, que cuantifica la presencia del patrón detectado en diferentes regiones de la imagen. Una propiedad fundamental de este mecanismo es la invarianza al desplazamiento, que permite reconocer un mismo patrón independientemente de su ubicación. Es importante señalar que esta propiedad se manifiesta de manera estricta únicamente cuando la convolución se realiza con un tamaño de paso igual a uno.

Los filtros que aprende una red convolucional pueden compararse con operadores clásicos de detección de bordes, como Sobel o Scharr, capaces de identificar direcciones verticales u horizontales. Sin embargo, la principal ventaja de las redes convolucionales es que los filtros no se definen manualmente, sino que sus valores se aprenden automáticamente mediante el algoritmo de backpropagation. Gracias a ello, el modelo adquiere la capacidad de descubrir patrones mucho más complejos y adaptados a la tarea específica.

A medida que la información avanza a través de las capas convolucionales, el tamaño espacial de las representaciones disminuye mientras que el número de canales se incrementa. Este proceso permite capturar progresivamente patrones de mayor nivel de abstracción, que van desde contornos simples hasta estructuras semánticamente significativas. Finalmente, las capas totalmente conectadas integran la información extraída para producir la predicción final, que puede consistir en clasificar una imagen, reconocer un objeto o identificar un rostro.

5.4. Componentes de una capa convolucional

El uso de convoluciones en redes neuronales introduce una serie de elementos esenciales que determinan el comportamiento y la eficacia del modelo. Uno de ellos es el relleno (padding), que consiste en añadir bordes artificiales alrededor de la imagen para evitar la pérdida de información en los márgenes y mantener las dimensiones originales de la entrada. Este procedimiento resulta necesario porque, a medida que se aplican operaciones de convolución, las dimensiones de las representaciones intermedias tienden a reducirse respecto a la imagen inicial. El relleno garantiza que el tamaño de salida coincida con el de entrada, lo que permite preservar información espacial en las etapas iniciales del procesamiento.

Otro concepto clave es el desplazamiento (stride), que define el número de píxeles que el filtro avanza en cada paso al recorrer la imagen. Un valor de stride mayor reduce las dimensiones de la salida y, en consecuencia, disminuye el número de cálculos necesarios. Cuando el tamaño del stride coincide con el del filtro, el proceso es equivalente a dividir la imagen en fragmentos independientes (patches), lo que aísla secciones completas y permite analizarlas de manera separada.

En el caso de imágenes en color, los filtros no se limitan a ser matrices bidimensionales, sino que se extienden a tres dimensiones para recorrer simultáneamente los canales rojo, verde y azul. Este aspecto resulta especialmente relevante porque el número de parámetros de una capa convolucional depende únicamente del tamaño y la cantidad de filtros, y no de las dimensiones de la imagen de entrada. De este modo, se logra una gran eficiencia en comparación con las redes totalmente conectadas. Por ejemplo, una capa con 10 filtros de 3 × 3 × 3 requiere solo 280 parámetros, cifra muy reducida frente a los millones de conexiones que implicaría una arquitectura densa de tamaño equivalente.

No obstante, conviene señalar que, al introducir variaciones como stride, padding o capas densas posteriores, se puede perder parcialmente la invarianza al desplazamiento que caracteriza a la convolución estándar con stride igual a uno. En consecuencia, una misma imagen trasladada circularmente hacia la izquierda o la derecha no siempre genera representaciones idénticas a las de la imagen original.

Las convoluciones resultan efectivas por dos motivos principales. En primer lugar, permiten una reducción drástica del número de parámetros, lo que simplifica el entrenamiento y reduce el riesgo de sobreajuste. En segundo lugar, implementan la compartición de parámetros, ya que un patrón aprendido en una región de la imagen puede aplicarse en cualquier otra, lo que favorece la capacidad de generalización del modelo.

Tras la convolución, suele aplicarse una etapa de agrupamiento (pooling), destinada a reducir las dimensiones intermedias y aportar robustez frente a pequeñas variaciones espaciales. Esta operación contribuye, en muchos casos, a recuperar parcialmente la invarianza al desplazamiento. La técnica más extendida es el max pooling, que selecciona el valor máximo dentro de cada región, priorizando la detección de la presencia de una característica por encima de su ubicación exacta. Otra variante frecuente es el average pooling, que sustituye cada región por el valor promedio de sus elementos, ofreciendo una representación más suavizada de la información.

5.5. Redes neuronales residuales, arquitecturas Inception y modelos móviles

El incremento en la profundidad de las redes neuronales ha permitido avances significativos en la visión computacional. Sin embargo, este aumento también genera un problema conocido. A partir de cierto punto, el rendimiento no mejora, sino que se degrada. La causa principal radica en fenómenos como la desaparición o explosión de gradientes, que dificultan el ajuste de los parámetros durante el entrenamiento y limitan la capacidad de la red para aprender de manera efectiva.

La solución a este desafío surgió con la introducción de las redes residuales (ResNet). Estas arquitecturas incorporan conexiones de atajo (skip connections), que transmiten directamente las activaciones de una capa hacia otra más profunda, como si se establecieran puentes dentro de la red. En consecuencia, cada bloque residual no aprende únicamente una transformación completa, sino la diferencia (residuo) entre la entrada y la salida esperada. Este diseño facilita el flujo de gradientes, permite entrenar redes mucho más profundas y marcó un hito en el desarrollo de la visión computacional, siendo la base de numerosos modelos posteriores.

Otra innovación relevante fue la arquitectura Inception, implementada en modelos como GoogLeNet. Su principio fundamental consiste en aplicar en paralelo filtros de distintos tamaños (1×1, 3×3 y 5×5), junto con una operación de pooling, y concatenar los resultados obtenidos. Esta estrategia permite capturar información a diferentes escalas espaciales, favoreciendo la detección de patrones tanto locales como globales. Para controlar el coste computacional asociado a este diseño, se introdujeron convoluciones de 1×1 que actúan como cuellos de botella, reduciendo la dimensionalidad de los datos antes de aplicar filtros más grandes. De este modo, la arquitectura logra un equilibrio entre expresividad y eficiencia.

Con la expansión de los dispositivos móviles y las aplicaciones en tiempo real, surgió la necesidad de arquitecturas más livianas y rápidas. En este contexto aparecieron las MobileNet, basadas en el concepto de convoluciones separables en profundidad. Este enfoque divide el proceso en dos etapas:

Convolución en profundidad (depthwise convolution): Cada filtro se aplica de manera independiente a un canal de la entrada.
Convolución puntual (1×1, pointwise convolution): Combina los resultados de todos los canales para generar una representación integrada.

Gracias a esta separación, se logra una reducción drástica en el número de operaciones y parámetros, lo que convierte a MobileNet en una arquitectura altamente eficiente.

La segunda generación, MobileNetV2, incorporó conexiones residuales junto con capas de expansión mediante filtros 1×1, que permiten aumentar la capacidad de representación sin comprometer la eficiencia.

5.6. Detección de objetos

En muchas aplicaciones de la visión computacional, como la conducción autónoma o la vigilancia inteligente, no basta con clasificar una imagen en su conjunto. Es imprescindible identificar qué objetos aparecen en la escena y en qué lugar se encuentran. Este desafío se aborda mediante la detección de objetos, un problema que combina simultáneamente la clasificación y la localización de los elementos presentes a través de recuadros delimitadores (bounding boxes).

En el caso más simple, se entrena un modelo para detectar un único objeto en cada imagen. Este modelo debe predecir tres aspectos fundamentales:

La probabilidad de presencia del objeto.
Las coordenadas del recuadro delimitador.
La clase a la que pertenece el objeto detectado.

Sin embargo, la mayoría de escenarios reales presentan múltiples objetos de diferentes clases y tamaños. Para abordar esta complejidad, una estrategia habitual consiste en dividir la imagen en una malla de celdas, donde cada celda se encarga de predecir la presencia de objetos cuyo centro se encuentra en su interior, junto con las coordenadas y la categoría correspondiente.

Uno de los algoritmos más influyentes en este ámbito es YOLO (You Only Look Once), que aplica la red convolucional a toda la imagen de manera simultánea. Gracias a este diseño, el modelo puede realizar detecciones en tiempo real, lo que lo convierte en una solución idónea para aplicaciones prácticas donde la velocidad es un requisito crítico.

El desempeño de los modelos de detección se evalúa y optimiza mediante diferentes métricas y técnicas:

Intersección sobre Unión (IoU): Mide la calidad de la predicción comparando el grado de solapamiento entre la caja predicha y la caja real. Un valor más alto de IoU indica una localización más precisa.
Supresión de No Máximos (NMS): Elimina predicciones redundantes en torno a un mismo objeto, conservando únicamente la más confiable.
Cajas de Anclaje (anchor boxes): Permiten que cada celda prediga múltiples objetos con distintas proporciones y escalas. Estas cajas se definen habitualmente a partir de algoritmos de agrupamiento, como k-means, que identifican formas y tamaños más representativos en los datos de entrenamiento.

Además de la detección convencional basada en recuadros, existen variantes del problema orientadas a tareas más específicas. Entre ellas destacan:

Detección de puntos de referencia: En lugar de delimitar áreas rectangulares, se predicen coordenadas concretas, como las posiciones de rasgos faciales o articulaciones en el cuerpo humano.
Métodos basados en regiones: Generan propuestas de posibles áreas de interés en la imagen, que posteriormente se clasifican. Este enfoque suele lograr mayor precisión, aunque con un coste computacional más elevado.

5.7. Segmentación semántica, convoluciones transpuestas y la arquitectura U-Net

La segmentación semántica constituye una de las tareas más avanzadas de la visión computacional, ya que no se limita a identificar qué objetos aparecen en una imagen, sino que asigna una clase específica a cada píxel. El resultado es un mapa detallado que representa con precisión la forma y extensión de cada objeto presente en la escena. Esta técnica resulta fundamental en campos como la medicina, donde se emplea para delimitar órganos o tumores en imágenes médicas, en la agricultura, para el análisis de cultivos, y en la robótica, para la percepción precisa del entorno.

Para alcanzar este nivel de detalle, es necesario reconstruir la resolución espacial original de la imagen a partir de representaciones comprimidas obtenidas en las etapas iniciales de la red. Esta tarea se logra mediante la convolución transpuesta, también conocida como deconvolución. A diferencia de la convolución tradicional, que reduce progresivamente las dimensiones espaciales, la convolución transpuesta expande dichas dimensiones, incrementando la resolución hasta aproximarse a la escala original de la entrada.

Un hito en este ámbito lo constituye la arquitectura U-Net, diseñada inicialmente para aplicaciones médicas, pero posteriormente adoptada en numerosos contextos. Esta arquitectura se estructura en dos fases principales:

Etapa de compresión (encoder): Reduce la resolución de la imagen y aumenta el número de canales, con el objetivo de extraer representaciones cada vez más abstractas y ricas en información semántica.
Etapa de expansión (decoder): Recupera la resolución original mediante convoluciones transpuestas, reconstruyendo la información espacial a partir de las características extraídas.

Para mitigar la pérdida de detalles espaciales ocasionada por la compresión, U-Net incorpora conexiones de omisión (skip connections), que transfieren información directamente desde las capas de compresión a las capas de expansión correspondientes. Gracias a estas conexiones, la red conserva detalles finos de bordes y contornos, alcanzando segmentaciones de alta precisión.

La salida de una arquitectura de segmentación puede variar según el problema abordado. En casos simples, puede consistir en un único recuadro, en otros, en un conjunto de coordenadas (por ejemplo, 2·n para la localización de n puntos de referencia), y en aplicaciones más complejas, en una máscara completa de segmentación que clasifica cada píxel de manera independiente.

5.8. One-Shot Learning

El cerebro humano posee una notable capacidad para reconocer objetos a partir de muy pocos ejemplos, fenómeno conocido como few-shot o one-shot learning. Esta habilidad se sustenta en dos mecanismos principales. Primero, la generación de representaciones jerárquicas generalizables, que no dependen de la memorización exacta de píxeles, sino de la extracción de características abstractas como formas, colores, movimientos y estructuras espaciales. Estas representaciones se construyen progresivamente a lo largo de la jerarquía cortical, de V1 a IT, donde las regiones superiores codifican objetos completos y conceptos visuales. Segundo, la asociación de estas representaciones con memoria y significado, mediante la interacción con áreas como la corteza prefrontal, el hipocampo y otras estructuras del sistema límbico, permite reconocer un objeto previamente visto incluso cuando se presenta en condiciones distintas de orientación, tamaño o estilo visual.

Los modelos de visión por computador suelen requerir grandes volúmenes de datos para alcanzar un entrenamiento eficaz. Sin embargo, en numerosos escenarios prácticos solo se dispone de un número muy reducido de ejemplos por clase. Este desafío se aborda mediante técnicas como el One-Shot Learning (aprendizaje con una sola muestra) o el Few-Shot Learning (aprendizaje con pocas muestras), que buscan dotar a los sistemas de la capacidad de generalizar a partir de datos escasos.

El principio fundamental de estos enfoques consiste en aprender un espacio de representación en el que las imágenes similares se ubiquen próximas entre sí, mientras que las correspondientes a clases distintas aparezcan más alejadas. La proximidad o distancia entre representaciones puede evaluarse con métricas como la distancia euclidiana, aunque también se emplean otras funciones de similitud más sofisticadas según el problema.

Una de las arquitecturas más representativas en este ámbito son las redes siamesas, que procesan en paralelo dos imágenes mediante una misma red convolucional que comparte parámetros. El resultado son vectores de características que pueden compararse directamente para decidir si ambas imágenes pertenecen o no a la misma clase. Este diseño permite que la red aprenda relaciones de similitud sin necesidad de entrenar un clasificador rígido para cada categoría.

Otra estrategia ampliamente utilizada en este contexto es la basada en la pérdida triple (triplet loss), que organiza el entrenamiento a partir de tríos de imágenes:

Anchor: La imagen de referencia.
Positiva: Una imagen de la misma clase que el anchor.
Negativa: Una imagen de una clase distinta.

El objetivo de esta función de pérdida es reducir la distancia entre el anchor y la muestra positiva, al tiempo que incrementa la distancia entre el anchor y la negativa. Este mecanismo genera representaciones más robustas y discriminativas, capaces de capturar similitudes profundas entre las imágenes.

Las aplicaciones del One-Shot Learning son amplias y de gran relevancia. En el reconocimiento facial, por ejemplo, permite identificar personas a partir de una sola fotografía de referencia. En el ámbito médico se emplea para la clasificación de enfermedades raras, donde es difícil disponer de grandes bases de datos. Asimismo, resulta útil en la identificación de especies poco comunes en biología o en tareas de clasificación en las que los datos disponibles son limitados.

5.9. Aprendizaje contrastivo y autosupervisado

El aprendizaje autosupervisado ocupa un lugar central en el ámbito de la visión por computador, ya que permite entrenar modelos robustos sin la necesidad de disponer de grandes volúmenes de datos etiquetados. Este enfoque se fundamenta en la generación automática de señales de supervisión a partir de los propios datos, lo que reduce de manera significativa la dependencia de procesos de anotación manual.

Dentro de este paradigma, una de las estrategias más influyentes es la que emplea la pérdida contrastiva. Su propósito es aprender un espacio de representación en el que las imágenes similares se ubiquen próximas entre sí, mientras que aquellas que difieren se sitúen a mayor distancia. Para lograrlo, se construyen pares de datos que se utilizan durante el proceso de optimización.

En escenarios sin etiquetas, los pares positivos se generan mediante transformaciones aplicadas a una misma imagen, tales como rotaciones, cambios de escala, recortes aleatorios o modificaciones en el color. De este modo, el modelo aprende que diferentes vistas de un mismo contenido deben compartir una representación cercana. Por el contrario, las imágenes distintas se consideran pares negativos, lo que obliga al modelo a situar sus representaciones en regiones alejadas del espacio embebido.

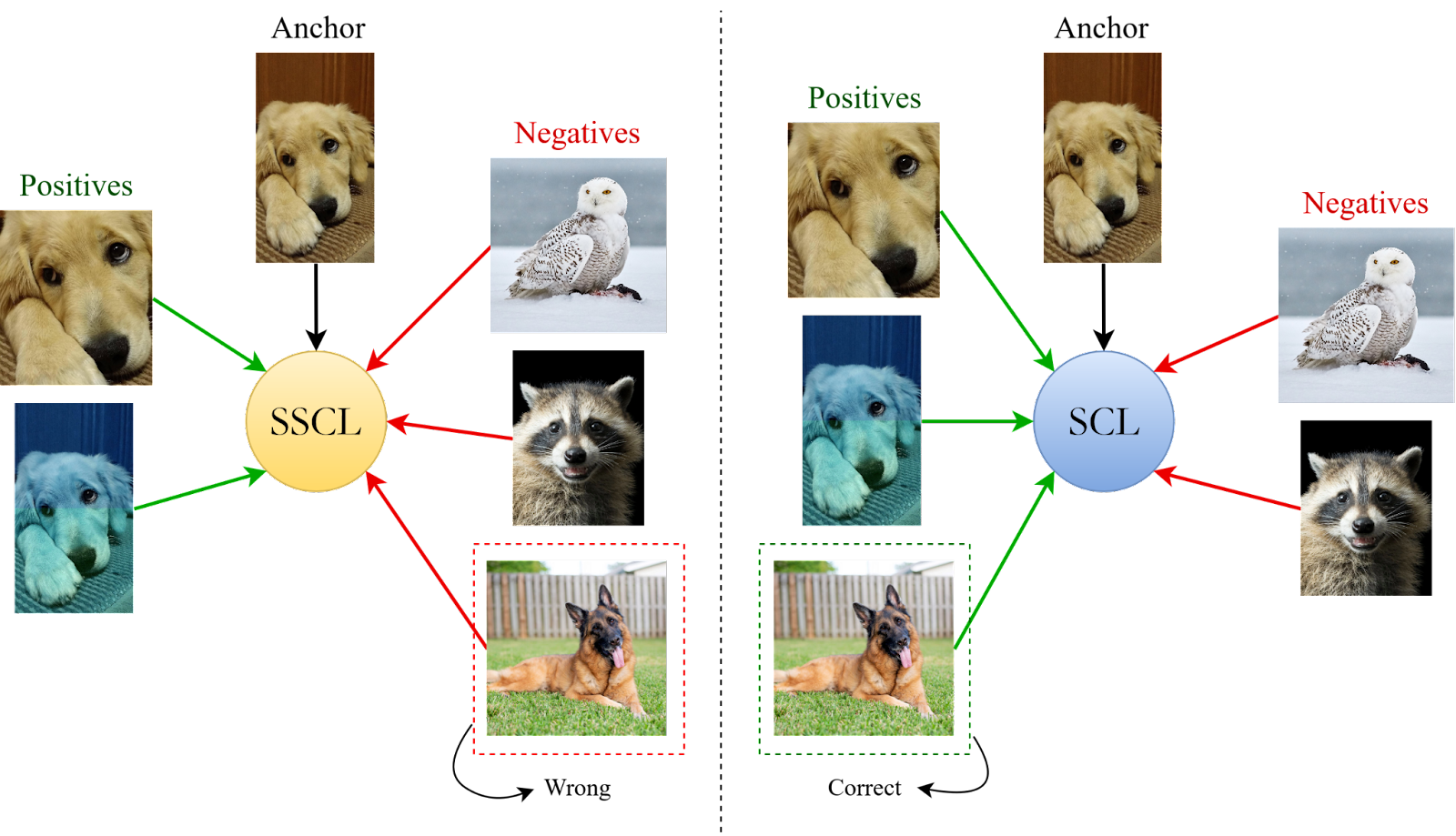
Ejemplo de aprendizaje contrastivo

El aprendizaje contrastivo no se corresponde de manera directa con el meta-learning, aunque contribuye a mejorar la calidad de las representaciones aprendidas por los modelos de aprendizaje profundo. Su objetivo principal consiste en agrupar en el espacio embebido las representaciones de datos similares y separar de manera efectiva aquellas que pertenecen a clases distintas. En aplicaciones de visión computacional, este principio se materializa mediante transformaciones de los datos que permiten al modelo reconocer que ciertas variaciones no alteran la esencia de la información original. Esto incrementa la comprensión semántica y refuerza la capacidad del modelo para generalizar ante datos fuera de distribución.

El proceso de entrenamiento contrastivo constituye una metodología clave para obtener representaciones efectivas y discriminativas a partir de datos no etiquetados. Dicho proceso incluye varias etapas esenciales que, combinadas con técnicas de fine-tuning y transfer learning, optimizan el rendimiento de los modelos:

Obtención de un conjunto de datos no etiquetados: Se establece la base sobre la cual el modelo aprende de manera automática las características más relevantes.
Generación de embeddings: Se emplea un modelo preentrenado, como una red neuronal profunda ajustada previamente con grandes volúmenes de datos, por ejemplo ResNet en visión computacional. Este modelo transforma las entradas en representaciones de menor dimensionalidad que preservan la información esencial, como bordes, texturas o patrones semánticos.
Optimización mediante fine-tuning: Se ajustan los parámetros del modelo utilizando medidas de distancia entre embeddings, como la distancia euclidiana o la similitud de coseno. El objetivo es minimizar la pérdida contrastiva, que busca reducir la distancia entre representaciones de datos similares y aumentar la separación respecto de las representaciones de datos distintos. Entre las funciones de pérdida más empleadas destacan la Triplet Loss, que considera un ancla, un par positivo y un par negativo, y la InfoNCE Loss, ampliamente utilizada en entornos no supervisados. Un aspecto crítico consiste en evitar el colapso de las representaciones, situación en la que todos los embeddings se vuelven indistinguibles. Para prevenirlo, se introducen márgenes o restricciones que aseguran diferencias suficientes entre clases.
Iteración y ajuste manual: Una vez entrenado el modelo, se revisan las muestras que generan mayores pérdidas. En casos necesarios, estas muestras se etiquetan manualmente, lo que refina el desempeño del modelo. Este ciclo iterativo favorece una mejora progresiva de las predicciones y reduce la necesidad de intervención humana con el tiempo.

Este proceso se apoya en los principios del transfer learning, que permiten reutilizar el conocimiento aprendido en una tarea fuente $T_a$ para mejorar el desempeño en una tarea objetivo $T_b$ . En lugar de comenzar el entrenamiento desde cero, se aprovechan las características generales aprendidas en la tarea inicial, lo que reduce la carga computacional y acelera el entrenamiento. Incluso cuando las distribuciones de datos en $T_a$ y $T_b$ difieren, dichas características resultan útiles al encapsular información fundamental como bordes, texturas o relaciones semánticas. En determinados casos, el ajuste fino no se limita a la capa final del modelo. Estudios como el Surgical Fine-Tuning demuestran que refinar de manera selectiva las capas intermedias puede incrementar significativamente la precisión.

El aprendizaje contrastivo se ha convertido en un componente esencial para mejorar la calidad de las representaciones en múltiples dominios, especialmente en visión computacional y procesamiento del lenguaje natural. A continuación, se describen algunas de las funciones de pérdida más utilizadas.

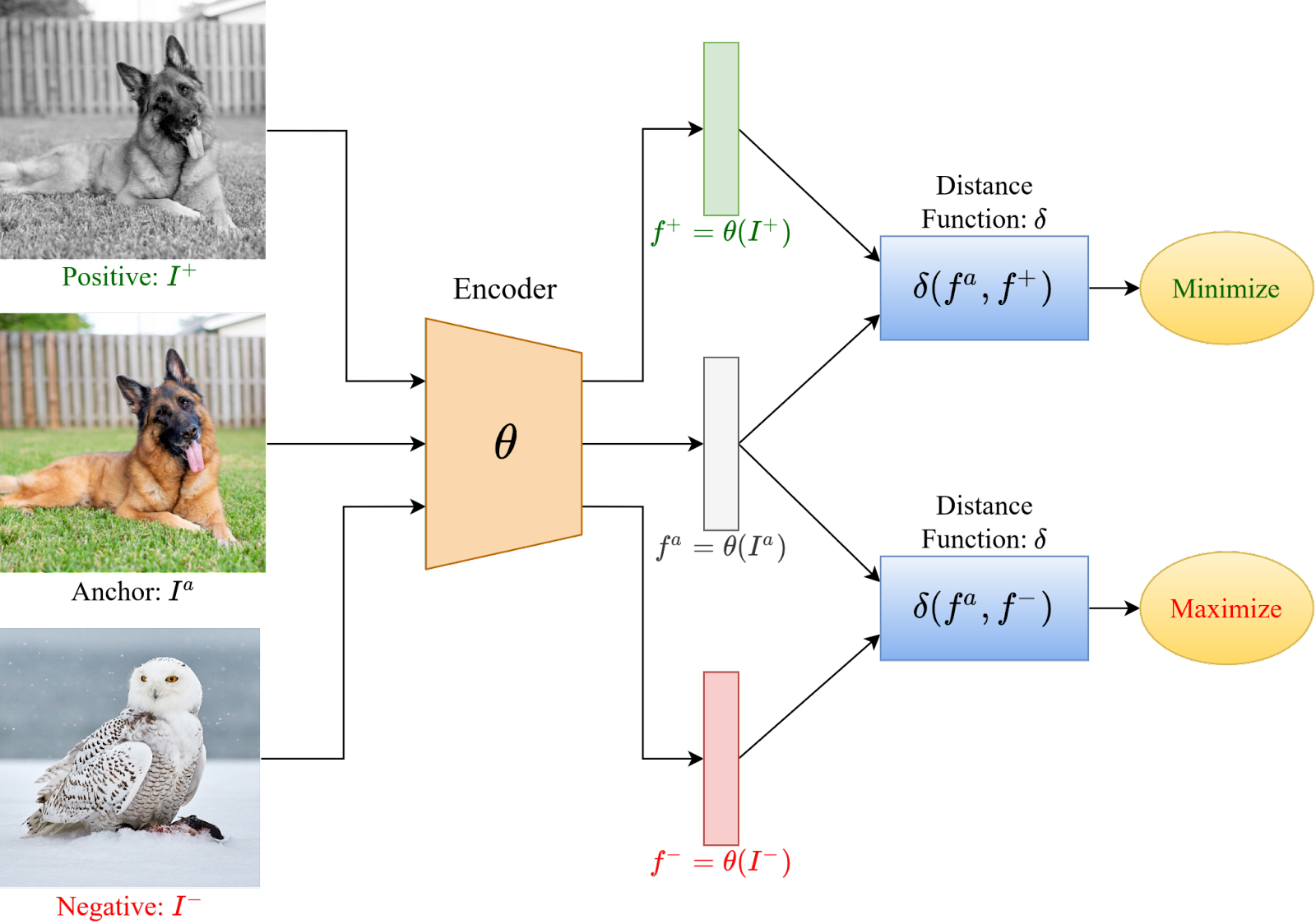
Ejemplo de Triplet Loss

La Triplet Loss se fundamenta en tres elementos principales:

Ancla ( $X$ ): Una muestra de datos que sirve como referencia.
Par positivo ( $X^+$ ): Una muestra similar al ancla, ya sea porque pertenece a la misma clase o porque corresponde a una transformación de esta.
Par negativo ( $X^-$ ): Una muestra distinta al ancla, normalmente perteneciente a otra clase.

El objetivo de la Triplet Loss es minimizar la distancia entre el ancla y el par positivo, a la vez que se maximiza la distancia entre el ancla y el par negativo. Matemáticamente, se expresa como:

L = \min_{\theta}\left(\max\left(0, \text{dist}(X, X^+) - \text{dist}(X, X^-) + \text{margen}\right)\right),

donde $\text{dist}(\cdot, \cdot)$ corresponde a una función de distancia, como la euclidiana o la similitud coseno, y el margen es un valor positivo que determina cuánto mayor debe ser la separación entre el ancla y el par negativo respecto de la distancia entre el ancla y el par positivo. Esta condición evita el colapso de las representaciones, garantizando que los pares negativos permanezcan adecuadamente diferenciados de los positivos.

La Contrastive Loss constituye otra función central en este campo, aunque se aplica a pares de datos en lugar de tríos. Su formulación es:

L = (1 - y) \frac{1}{2} \left( \text{dist}(X_1, X_2) \right)^2 + y \frac{1}{2} \left( \max(0, m - \text{dist}(X_1, X_2)) \right)^2,

donde $y$ indica si $X_1$ y $X_2$ son similares ( $y = 0$ ) o distintos ( $y = 1$ ), $m$ representa el margen mínimo deseado entre ejemplos diferentes, y $\text{dist}(X_1, X_2)$ suele calcularse con la distancia euclidiana. En este caso, los ejemplos similares se obligan a aproximarse en el espacio embebido, mientras que los diferentes deben separarse al menos una distancia equivalente al margen $m$ .

Finalmente, la InfoNCE Loss (Noise-Contrastive Estimation) se utiliza de manera destacada en arquitecturas como SimCLR. Su objetivo es maximizar la similitud entre un dato ancla y su par positivo, mientras se minimiza la similitud con los pares negativos presentes en el mismo lote de datos. La fórmula se define como:

L = -\frac{1}{N} \sum_{i=1}^N \log \frac{\exp(\text{sim}(z_i, z_i^+)/\tau)}{\sum_{j=1}^K \exp(\text{sim}(z_i, z_j^-)/\tau)},

donde $z_i$ corresponde al embedding del ancla, $z_i^+$ al embedding del par positivo, $z_j^-$ a los embeddings de los pares negativos, $\text{sim}(\cdot, \cdot)$ a una medida de similitud como el producto escalar o la similitud coseno, y $\tau$ a una constante de temperatura que ajusta la distribución de probabilidades. Este mecanismo fomenta la generación de representaciones ricas y diferenciadas, adecuadas para tareas de clasificación o transferencia.

Limitaciones del aprendizaje contrastivo

Dependencia de transformaciones adecuadas: El rendimiento requiere el diseño cuidadoso de técnicas de aumento de datos, como resizes, crops, modificaciones de color, CutMix o MixUp, que mejoren la robustez del modelo.
Necesidad de un gran número de épocas: El desempeño depende tanto del tamaño de los lotes como del número de iteraciones necesarias para obtener suficientes pares negativos efectivos.

6. Arquitecturas de aprendizaje profundo, modelos secuenciales

Muchos problemas en inteligencia artificial se caracterizan por involucrar datos secuenciales, es decir, información organizada en un orden temporal o lógico. Ejemplos destacados incluyen el reconocimiento de voz, la generación de música, el análisis de sentimientos en texto, la interpretación de secuencias de ADN o la traducción automática de idiomas. A diferencia de las imágenes, donde la información espacial es clave, en las secuencias la dependencia entre elementos previos y posteriores resulta esencial. Para abordar este tipo de problemas se emplean los modelos secuenciales, cuya función es procesar los datos respetando su orden y capturando las dependencias que existen a lo largo de la secuencia.

6.1. Representación de secuencias

En el procesamiento del lenguaje natural, las palabras deben transformarse en representaciones que puedan ser interpretadas por un modelo. Este procedimiento se denomina tokenización. Consiste en asignar a cada palabra un índice único dentro de un diccionario y, posteriormente, transformarla en un vector que codifica su información.

El proceso de tokenización contempla también el uso de tokens especiales. Entre ellos se incluyen:

Un token reservado para representar palabras desconocidas o no registradas en el vocabulario.
Un token de fin de secuencia, empleado en tareas de generación de texto para señalar el cierre de la frase.

Las secuencias de entrada y salida no siempre poseen la misma longitud, lo que obliga a gestionar variables específicas que reflejen estos tamaños y permitan al modelo adaptarse a diferentes contextos. Este tratamiento cuidadoso de la representación resulta esencial para que los modelos secuenciales puedan captar correctamente la estructura y el significado del lenguaje, así como de cualquier otro tipo de datos organizados en secuencia.

6.2. Redes neuronales recurrentes

Las redes neuronales recurrentes (Recurrent Neural Networks, RNN) constituyen una extensión de las redes tradicionales diseñada para procesar datos secuenciales. Su principal característica es la capacidad de recordar información previa, ya que reutilizan la salida de un paso anterior como parte de la entrada en el siguiente. En cada instante temporal, la red combina la entrada actual con el estado oculto anterior para generar un nuevo estado oculto y producir una salida.

Este mecanismo permite que los parámetros se compartan a lo largo de la secuencia, lo que no solo reduce el número de variables que deben aprenderse, sino que también posibilita que la predicción en un momento dado tenga en cuenta el contexto acumulado de los pasos previos. Gracias a esta propiedad, las RNN resultan adecuadas para tareas donde el orden de los elementos y las dependencias temporales son fundamentales, como en la traducción automática, el modelado del lenguaje o el análisis de series temporales.

No obstante, en la práctica las RNN se enfrentan a dos problemas significativos:

Desvanecimiento de gradientes: Durante el entrenamiento, los gradientes asociados a pasos muy lejanos en la secuencia tienden a volverse extremadamente pequeños, lo que dificulta que el modelo aprenda dependencias a largo plazo.
Explosión de gradientes: En algunos casos, los gradientes crecen de manera descontrolada, afectando la estabilidad del entrenamiento e impidiendo la convergencia del modelo.

Para superar estas limitaciones, se desarrollaron variantes más sofisticadas y robustas:

RNN bidireccionales: Procesan la secuencia tanto en la dirección hacia adelante como hacia atrás, integrando simultáneamente información del pasado y del futuro, lo que resulta especialmente útil en tareas donde el contexto completo de la secuencia es relevante.
LSTM (Long Short-Term Memory): Introducen una estructura de celdas de memoria acompañada de puertas de control que regulan qué información se conserva, cuál se descarta y cuál se utiliza en cada paso. Esta arquitectura permite capturar dependencias a largo plazo de manera eficaz, mitigando el problema del desvanecimiento de gradientes.
GRU (Gated Recurrent Unit): Constituyen una variante simplificada de las LSTM. Mantienen el uso de puertas para controlar el flujo de información, pero con una estructura más ligera y eficiente en términos computacionales, alcanzando un rendimiento comparable en muchos contextos sin requerir tanta capacidad de cómputo.

6.3. Modelos de lenguaje y predicción de secuencias

Los modelos de lenguaje son sistemas diseñados para asignar probabilidades a secuencias de palabras, permitiendo predecir la siguiente palabra en un texto dado el contexto previo. Su entrenamiento se realiza a partir de grandes corpus, con el objetivo de que el modelo aprenda no solo asociaciones entre palabras, sino también patrones gramaticales, sintácticos y contextuales. Este aprendizaje habilita una amplia variedad de aplicaciones, tales como asistentes virtuales, análisis de emociones en texto, generación automática de contenido y descifrado o interpretación de secuencias genéticas, donde la dependencia entre elementos consecutivos es crucial.

6.4. Representación de palabras y la revolución de los Transformers

En el procesamiento del lenguaje natural (Natural Language Processing, NLP), un concepto central es el de los word embeddings, que son vectores densos que representan palabras en un espacio continuo. En este espacio, las relaciones semánticas entre palabras se reflejan en la geometría, donde palabras con significados similares se ubican cerca, y las analogías pueden representarse mediante operaciones vectoriales. Este enfoque supera al one-hot encoding, que asigna a cada palabra un vector binario sin reflejar relaciones semánticas ni similitudes contextuales.

El aprendizaje de embeddings puede realizarse mediante diferentes técnicas:

Word2Vec: Entrena modelos para predecir palabras a partir de su contexto en ventanas de texto, utilizando estrategias como negative sampling para reforzar la relevancia de las relaciones semánticas aprendidas.
GloVe: Combina información de coocurrencia global de palabras con factorización de matrices, integrando tanto la información local de contexto como la estadística global del corpus, lo que permite generar representaciones más consistentes y ricas semánticamente.

Estas representaciones pueden preentrenarse en grandes corpus y transferirse a tareas específicas, lo que facilita la generalización y reduce la necesidad de datos etiquetados en contextos concretos. Sin embargo, es importante señalar que los embeddings también reflejan sesgos presentes en los datos de entrenamiento, los cuales pueden afectar el comportamiento de los modelos. Estos sesgos pueden identificarse y mitigarse mediante técnicas de neutralización o ajuste post-entrenamiento, garantizando que las aplicaciones resultantes sean más justas y confiables.

El desarrollo de embeddings sentó las bases para la revolución de los Transformers, que introducen mecanismos de atención capaces de modelar dependencias a largo plazo de manera eficiente, desplazando gradualmente a las arquitecturas recurrentes tradicionales en muchas tareas de NLP y secuencias en general.

6.5. Mecanismo de atención

El mecanismo de atención constituye un componente fundamental en las arquitecturas modernas de procesamiento de secuencias, ya que permite al modelo centrarse en las partes más relevantes de la entrada según la tarea a realizar. Este mecanismo se implementa a través de tres vectores:

Query (Q): Representa lo que se está buscando o la información a destacar en un momento determinado.
Key (K): Codifica la información disponible que puede ser relevante para la consulta.
Value (V): Contiene el contenido asociado que se utilizará para construir la representación final.

El funcionamiento consiste en comparar la Query con cada Key para calcular un conjunto de pesos que reflejan la relevancia relativa de cada elemento. A continuación, estos pesos se aplican a los Values correspondientes, generando representaciones contextuales que integran la información más significativa para la tarea específica. Este enfoque permite al modelo enfocarse dinámicamente en diferentes partes de la secuencia, mejorando la capacidad de capturar dependencias a largo plazo y relaciones complejas.

6.6. Transformers

Los Transformers, introducidos en el artículo Attention is All You Need, revolucionaron el procesamiento de secuencias al eliminar la necesidad de recurrir a RNN, permitiendo un procesamiento paralelo de los datos. La arquitectura se organiza en dos componentes principales:

Encoder: Procesa la secuencia de entrada y genera representaciones internas enriquecidas.
Decoder: Utiliza estas representaciones para generar la secuencia de salida de manera autoregresiva o condicional según la tarea.

Cada bloque del Transformer combina mecanismos de autoatención (self attention) y redes totalmente conectadas, lo que permite capturar relaciones complejas dentro de la secuencia. Dado que los Transformers no procesan los elementos de manera secuencial, se incorporan positional encodings para preservar información sobre el orden de los elementos, garantizando que la red pueda distinguir entre distintas posiciones en la secuencia.

El multi-head attention constituye una extensión clave del mecanismo de atención, ya que permite al modelo observar relaciones desde múltiples perspectivas simultáneamente. Esto enriquece la representación al capturar distintos tipos de dependencias y patrones contextuales en paralelo.

Gracias a estas innovaciones, los Transformers escalan de manera eficiente a secuencias largas, capturan dependencias complejas y se han extendido más allá del procesamiento de lenguaje natural hacia dominios como la visión computacional, la bioinformática y el aprendizaje por refuerzo, consolidándose como una de las arquitecturas más versátiles y poderosas en el aprendizaje profundo actual.

8. Arquitecturas de aprendizaje profundo, redes neuronales de grafos

Los grafos constituyen una estructura flexible y poderosa para representar información compleja. Están formados por nodos (o vértices) y aristas (o conexiones) que describen las relaciones existentes entre los elementos. Esta formalización permite modelar fenómenos muy diversos, desde redes sociales y moléculas hasta sistemas de telecomunicaciones, imágenes y texto, ofreciendo un marco unificado para el análisis de datos estructurados y relacionales.

Las Redes Neuronales de Grafos (Graph Neural Networks, GNN) están diseñadas para procesar directamente estas estructuras, extrayendo representaciones cada vez más ricas de los nodos y del grafo en su conjunto, de manera análoga a cómo las redes convolucionales procesan imágenes.

8.1. Representación de nodos y flujo de información

Cada nodo de un grafo se representa mediante un vector de características que codifica su información individual. Durante sucesivas iteraciones, este vector se actualiza combinando la información propia del nodo con la de sus vecinos, enriqueciendo así su representación con el contexto del grafo.

Dado que los grafos no poseen un orden natural de nodos o conexiones, las operaciones de agregación, como suma, promedio o máximo, deben ser conmutativas, garantizando que el resultado no dependa del orden en que se procesen los vecinos. Con cada iteración, los nodos adquieren representaciones que integran tanto sus propiedades individuales como las de su entorno inmediato, permitiendo al modelo capturar dependencias locales y globales de manera eficiente.

8.2. Representación de la estructura del grafo

La topología de un grafo puede representarse mediante distintas estructuras de datos:

Matriz de adyacencia: Indica la presencia o ausencia de aristas entre nodos. Su implementación es sencilla, pero su eficiencia depende del orden de los nodos y puede resultar costosa en grafos de gran tamaño.
Listas de adyacencia: Enumeran explícitamente las conexiones de cada nodo, ofreciendo mayor flexibilidad y eficiencia en el manejo de grafos dispersos.

En la práctica, estas representaciones se traducen en tensores que almacenan tanto las características de los nodos como las relaciones que los unen, constituyendo la base para las operaciones de propagación y actualización de las GNN.

8.3. Tareas sobre grafos

Las GNN permiten abordar problemas a diferentes niveles de granularidad:

Nivel de grafo: Predicción de propiedades globales, como la clasificación de moléculas, la estimación de propiedades químicas o el análisis de sentimiento de un texto completo.
Nivel de nodo: Identificación de roles o categorías de nodos, útil en segmentación de imágenes, detección de usuarios influyentes en redes sociales o categorización de palabras en grafos semánticos.
Nivel de arista: Predicción de la existencia o el valor de conexiones, aplicable en sistemas de recomendación, detección de enlaces en grafos de conocimiento o relaciones biológicas entre moléculas.

8.4. Arquitecturas y variantes

Entre las arquitecturas más destacadas se encuentran:

Graph Convolutional Networks (GCN): Cada nodo se actualiza a partir de la información agregada de sus vecinos, de manera análoga a las convoluciones en imágenes, permitiendo capturar patrones locales y globales en el grafo.
Graph Attention Networks (GAT): Incorporan un mecanismo de atención que pondera la relevancia relativa de cada vecino, mejorando la capacidad de la red para diferenciar relaciones críticas de otras menos importantes.

El flujo de información en una GNN se basa en el intercambio de mensajes entre nodos. En grafos muy grandes, este proceso puede resultar costoso, por lo que se introducen mecanismos como el nodo maestro (masternode), que centraliza la propagación de información global sin necesidad de mantener conexiones exhaustivas entre todos los nodos.

8.5. Aplicaciones

Los grafos ofrecen un marco unificado para abordar problemas en múltiples dominios:

Visión por computadora: Una imagen puede representarse como un grafo de nodos, donde cada nodo corresponde a un píxel o superpíxel, conectados según proximidad o similitud.
Lenguaje natural: Palabras de una oración o documento pueden organizarse como nodos en grafos secuenciales o semánticos, capturando relaciones contextuales y sintácticas.
Biología y química: Moléculas, proteínas o redes metabólicas se describen naturalmente como grafos de átomos y enlaces, permitiendo predecir propiedades químicas o interacciones biológicas.

9. Paradigmas de aprendizaje, Multi-task learning y meta learning

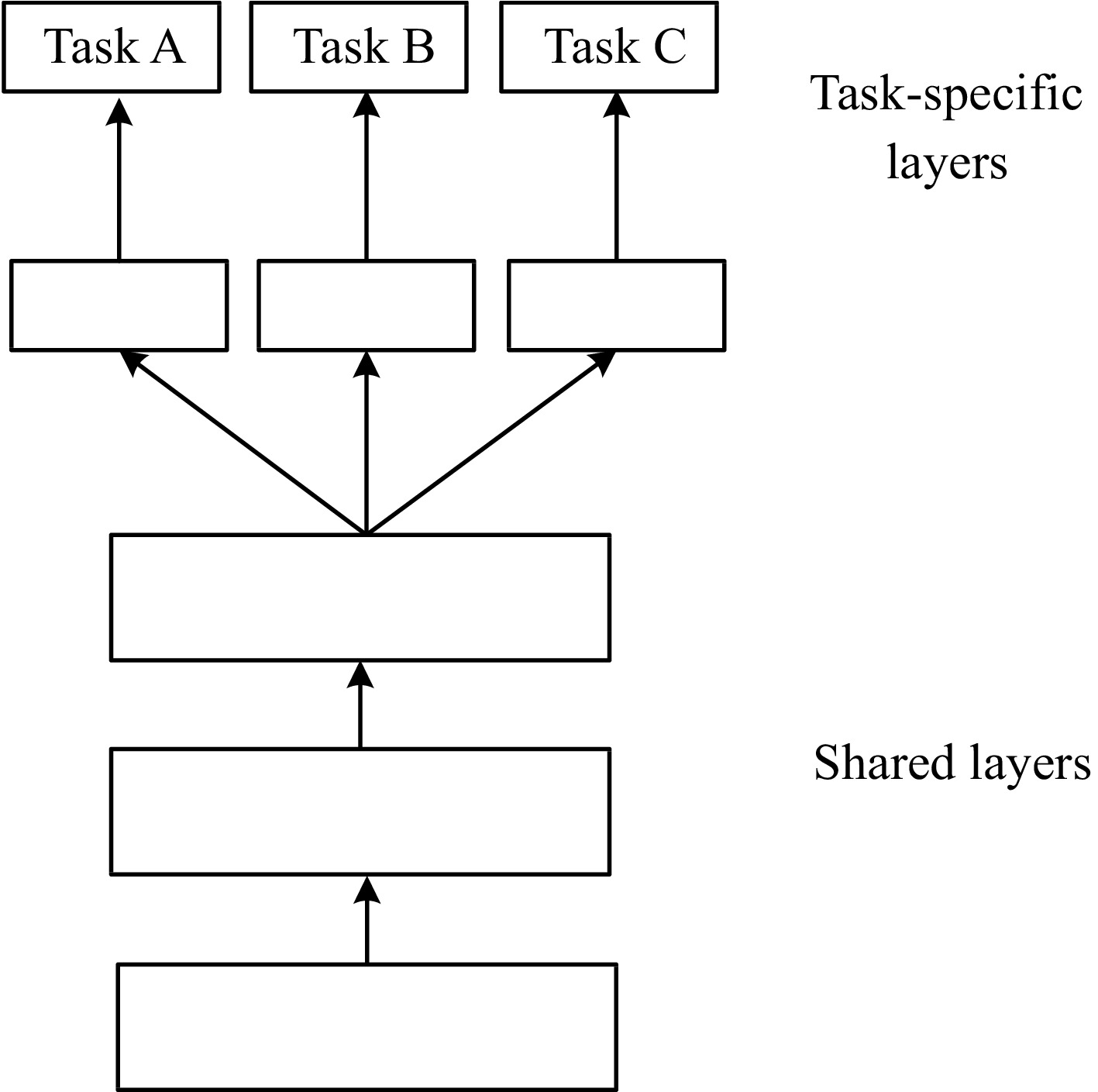
Diagrama de una arquitectura Multi-Task

El Multi-Task Learning (MTL) se refiere a la capacidad de un modelo para realizar múltiples tareas relacionadas de forma simultánea, utilizando una estructura compartida que permite adaptar parámetros y salidas según el entorno. Este enfoque busca optimizar recursos y mejorar la capacidad de generalización del modelo en escenarios dinámicos, transfiriendo conocimiento entre tareas y minimizando la necesidad de ajustes específicos.

Diagrama sobre el uso de Meta-Learning

El Meta-Learning se enfoca en dotar a los modelos de la habilidad de identificar y aprovechar patrones subyacentes en los datos, lo que les permite adaptarse rápidamente a nuevos problemas o entornos con un mínimo de información.

Este enfoque es particularmente útil en escenarios con datos limitados o costosos de obtener, como aquellos que involucran problemas de privacidad. Al mejorar la capacidad de generalización, los modelos son más robustos y eficientes, optimizando recursos y ofreciendo mejores resultados en tareas variadas.

Por tanto, resulta ideal para conjuntos de datos donde la proporción de datos etiquetados es significativamente menor que la de datos no etiquetados. El uso del paradigma de Meta-Learning permite extraer patrones de datos etiquetados y aplicarlos a datos no etiquetados, detectando variaciones y cambios en las distribuciones.

9.1. Parámetros en Multi-Task Learning

Al desarrollar modelos para multi-task learning, es crucial definir ciertos parámetros:

Parámetros aprendibles, $\theta$ : Representa todos los parámetros que el modelo puede aprender.
Función, $f_\theta(y|x)$ : Describe el modelo parametrizado $\theta$ , generando una distribución de probabilidad para $y$ dado $x$ .
Tarea, $T_i$ : Se define como $T_i = \{p_i(x), p_i(y|x), L_i\}$ $T_{i} = {p_{i} (x), p_{i} (y ∣ x), L_{i}}$ , donde:
- $p_i(x)$ : Distribución de entrada $x$ específica de la tarea $T_i$ .
- $p_i(y|x)$ : Distribución de probabilidad de la salida $y$ dado $x$ para la tarea $T_i$ .
- $L_i$ : Función de pérdida asociada con la tarea $T_i$ .

El objetivo general es minimizar la pérdida total del modelo a lo largo de todas las tareas. Esto se puede formular como

\min_{\theta} \sum_{i=1}^{T} L_i(\theta, D_i),

donde $D_i$ es el conjunto de datos de la tarea $i$ . Además, para ajustar la relevancia de cada tarea, se puede incluir un peso $w_i$

\min_{\theta} \sum_{i=1}^{T} w_i \cdot L_i(\theta, D_i).

9.2. Estrategias para Multi-Tasking

Las principales estrategias para abordar múltiples tareas incluyen:

Modelos específicos para cada tarea: Este enfoque no es escalable debido al alto costo computacional.
Uso de embeddings condicionales: Técnicas que combinan información mediante:
- Concatenación o suma de embeddings: Métodos equivalentes que combinan características.
- Sistemas Multi-head: Un modelo único con múltiples salidas, eficiente para tareas variadas. Un ejemplo avanzado es el Multi-Gate Mixture of Experts.
- Condicionales multiplicativos: Ajustan los embeddings mediante factores multiplicativos según la tarea.

9.3. Few-Shot Learning

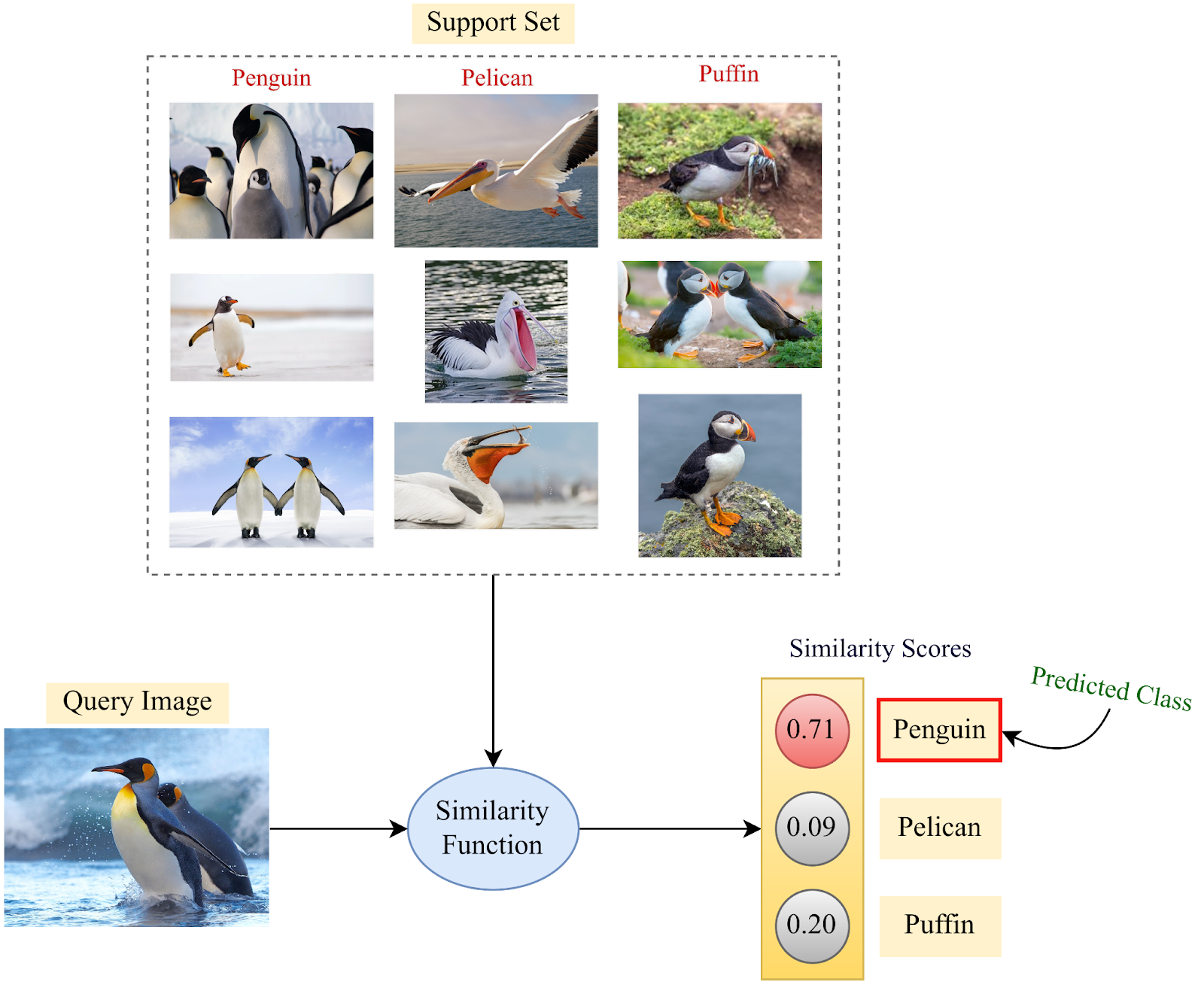
Ejemplo de uso de Few-Shot Learning de 3-ways y 3-shots

El Few-Shot Learning (FSL) se centra en entrenar modelos que logren un alto rendimiento con un número muy limitado de ejemplos etiquetados por clase. Este enfoque es esencial en situaciones donde la recopilación de datos es complicada o costosa, como en aplicaciones médicas o donde se requiere la privacidad de los datos.

El FSL se organiza en torno a dos conjuntos principales:

Support Set: Es el conjunto de datos de entrenamiento específico para una tarea, compuesto por unas pocas muestras etiquetadas que el modelo utiliza para aprender a clasificar.
Query Set: Es el conjunto de datos de prueba utilizado para evaluar el rendimiento del modelo en la misma tarea.

El aprendizaje few-shot se describe según dos parámetros importantes:

K-shot Learning: Se refiere al número $K$ de ejemplos disponibles por clase en el support set. Por ejemplo, en un escenario de 1-shot learning, hay solo un ejemplo por clase, mientras que en 5-shot learning hay cinco ejemplos por clase.
N-way Classification: Indica el número $N$ de clases diferentes en la tarea. Por ejemplo, un problema de 5-way classification implica clasificar entre cinco posibles categorías.

Existen dos tipos de modelos en este regimen:

Modelos no parametrizados: Métodos como k-Nearest Neighbors (k-NN) son simples y eficaces cuando se dispone de pocos datos. Sin embargo, su eficacia depende de tener embeddings de alta calidad que representen bien las relaciones entre los datos.
Modelos parametrizados: Redes neuronales profundas o métodos similares se utilizan para generar embeddings que capturan las características relevantes de los datos en un espacio de menor dimensionalidad, reduciendo problemas como la maldición de la dimensionalidad. Estos modelos se entrenan para producir representaciones invariantes a transformaciones y adecuadas para métodos como k-NN.

Bibliografía​

1. Introducción al aprendizaje profundo​

1.1. Predicción de precios de viviendas mediante regresión lineal​

1.2. Elementos esenciales de una neurona artificial​

1.3. Tipos de arquitecturas y datos​

1.4. Factores que impulsan su desarrollo​

2. Regresión lineal y logística​

2.1. Detección de gatos en imágenes mediante regresión logística​

2.2. Función de pérdida y coste​

2.3. Descenso del gradiente​

2.4. Implementación de la regresión logística​

3. Redes neuronales y funciones de activación​

3.1. Generalización y sobreajuste​

3.2. De neuronas a redes neuronales​

3.3. Funciones de activación​

3.4. Implementación de una red neuronal​

4. Introducción a las redes neuronales profundas​

4.1. Parámetros e hiperparámetros​

4.2. Propagación hacia delante​

4.3. Propagación hacia atrás y optimización​

4.3.1. Implementación de optimizadores​

4.4. División del conjuntos de datos​

4.5. Sesgo y varianza​

4.6. Métodos de regularización y normalización​

4.7. Desvanecimiento y explosión de gradientes​

4.8. Estrategia en el proceso de optimización​

4.9. Aprendizaje por transferencia y multitarea​

5. Arquitecturas de aprendizaje profundo, redes neuronales convolucionales​

5.1. Procesamiento visual humano y su analogía con las redes neuronales convolucinales​

5.2. Campo receptivo y jerarquía de procesamiento visual​

5.3. Conceptos fundamentales de la convolución​

5.4. Componentes de una capa convolucional​

5.5. Redes neuronales residuales, arquitecturas Inception y modelos móviles​

5.6. Detección de objetos​

5.7. Segmentación semántica, convoluciones transpuestas y la arquitectura U-Net​

5.8. One-Shot Learning​

5.9. Aprendizaje contrastivo y autosupervisado​

Limitaciones del aprendizaje contrastivo​

6. Arquitecturas de aprendizaje profundo, modelos secuenciales​

6.1. Representación de secuencias​

6.2. Redes neuronales recurrentes​

6.3. Modelos de lenguaje y predicción de secuencias​

6.4. Representación de palabras y la revolución de los Transformers​

6.5. Mecanismo de atención​

6.6. Transformers​

8. Arquitecturas de aprendizaje profundo, redes neuronales de grafos​

8.1. Representación de nodos y flujo de información​

8.2. Representación de la estructura del grafo​

8.3. Tareas sobre grafos​

8.4. Arquitecturas y variantes​

8.5. Aplicaciones​

9. Paradigmas de aprendizaje, Multi-task learning y meta learning​

9.1. Parámetros en Multi-Task Learning​

9.2. Estrategias para Multi-Tasking​

9.3. Few-Shot Learning​